动态规划基础

阶段：原问题划分为的若干子问题
状态：提取的每个子问题的特征
决策：寻找每个状态的可能
状态转移方程：各状态之间的相互转移方式

动态规划原理

动态规划，简称 DP。所有算法归根到底就是解决如何让计算机更聪明的枚举，动态规划亦如此。动态规划与分治法类似，基本思想也是将待求解问题分解成若干个子问题进行求解。但与分治法不同，动态规划的子问题之间不相互独立。

通常动态规划法仅解决每个子问题一次，使用一个表来记录每个状态。求当前状态一般会用到之前所求状态，可以直接查表获取。当前状态和之前状态之间的转移规律，称之为状态转移方程，动态规划最难的就是状态转移方程。

使用条件

能用动态规划解决的问题，需要满足条件：最优子结构，无后效性和子问题重叠。

最优子结构：最优解所包含的子问题的解也是最优的
无后效性：已经求解的子问题，不会再受到后续决策的影响
子问题重叠：对于有大量重叠子问题，可以存储这些子问题的解，避免重复求解相同的子问题，从而提升效率

基本思路

定义状态：根据求解的目标状态来定义数组目标状态涵盖所有变量 $DP[i][j]$。划分的阶段一定要是有序的或者是可排序的
**将原问题划分为若干子问题阶段**，提取这些子问题的特征状态
寻找状态转移方程：状态转移就是根据上一阶段的状态和决策来导出本阶段的状态

$$
DP[i][j] = Operation\left(DP[i-1][j],DP[i][j-1],\cdots\right)
$$

寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件
按顺序求解每阶段

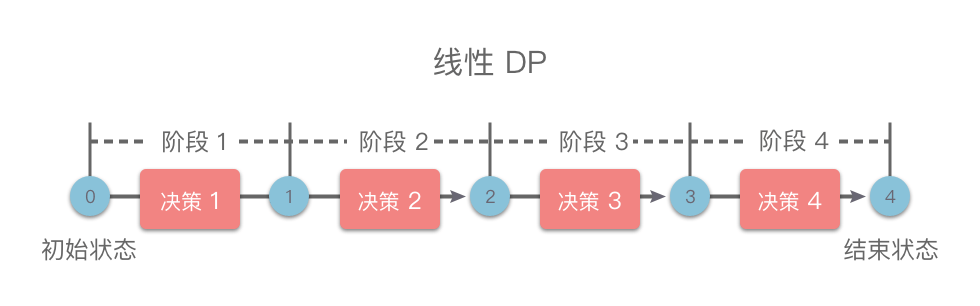
线性 DP

具有「线性」阶段划分的动态规划方法统称为线性动态规划。背包问题、区间 DP、数位 DP 等都属于线性 DP。

线性 DP 示例

背包 DP

背包问题是一类经典的动态规划问题，是一种组合优化的 NP 完全问题。NP 完全问题无多项式时间复杂度的解法，但是可以利用动态规划，以伪多项式时间复杂度求解。
问题描述：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

背包问题类型：详见背包问题

区间 DP

区间 DP 就是在一段区间上进行动态规划——并非以离散的点划分，而是以「区间长度」划分阶段，以两个坐标（区间的左、右端点）作为状态的维度。一个状态通常由被它包含且比它更小的区间状态转移而来。

主要思想：先在小区间内得到最优解，再利用小区间的最优解合并，从而得到大区间的最优解，最终得到整个区间的最优解。

从中间向两侧转移的区间 DP 问题

单个区间从中间向两侧更大区间转移的区间 DP 问题。比如从区间 $[i+1,j-1]$ 转移到更大区间 $[i,j]$

状态转移方程：

$$
dp[i][j]=\max\left{dp[i+1][j-1],dp[i+1][j],dp[i,j-1]\right}+cost[i][j],\ \ i\le j
$$

$dp[i][j]$：区间 $[i,j]$ 上最大值
$cost$：从小区间转移到区间 $[i,j]$ 的代价

基本步骤：

枚举区间的起点
枚举区间的终点
根据状态转移方程计算从小区间转移到更大区间后的最优值

for i in range(size - 1, -1, -1):       # 枚举区间起点
    for j in range(i + 1, size):        # 枚举区间终点
        dp[i][j] = max(dp[i + 1][j - 1], dp[i + 1][j], dp[i][j - 1]) + cost[i][j]  # # 状态转移方程，计算转移到更大区间后的最优值

多个小区间转到大区间的区间 DP 问题

多个小区间转移到大区间的区间 DP 问题。比如从区间 $[i,k]$ 和区间 $[k,j]$ 转移到区间 $[i,j]$

状态转移方程：

$$
dp[i][j] = \max\left{dp[i,k]+dp[k+1][j]+cost[i][j]\right}\ \ i<k<j
$$

$dp[i][j]$：区间 $[i,j]$ 上最大值
$cost$：将两个区间 $[i,k]$ 与 $[k+1][j]$ 中的元素合并为区间 $[i,j]$ 中的元素的代价

基本步骤：

枚举区间长度
枚举区间的起点，根据区间起点和区间长度得出区间终点
枚举区间的分割点，根据状态转移方程计算合并区间后的最优值

for l in range(1, n):               # 枚举区间长度
    for i in range(n):              # 枚举区间起点
        j = i + l - 1               # 根据起点和长度得到终点
        if j >= n:
            break
        dp[i][j] = float('-inf')    # 初始化 dp[i][j]
        for k in range(i, j + 1):   # 枚举区间分割点
            dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + cost[i][j])  # 状态转移方程，计算合并区间后的最优值