搜索

搜索，也就是对状态空间进行枚举，通过穷尽所有的可能来找到最优解，或者统计合法解的个数。

搜索简介

搜索有很多优化方式，如减小状态空间，更改搜索顺序，剪枝等。

搜索是一些高级算法的基础。在 OI 中，纯粹的搜索往往也是得到部分分的手段，但可以通过纯粹的搜索拿到满分的题目非常少。

DFS

DFS 为图论中的概念，详见 DFS（图论） 页面。在 搜索算法 中，该词常常指利用递归函数方便地实现暴力枚举的算法，与图论中的 DFS 算法有一定相似之处，但并不完全相同。

该类搜索算法的特点在于，将要搜索的目标分成若干「层」，每层基于前几层的状态进行决策，直到达到目标状态。

考虑上述问题，即将正整数 $n$ 分解成小于等于 $m$ 个正整数之和，且排在后面的数必须大于等于前面的数，并输出所有方案。

设一组方案将正整数 $n$ 分解成 $k$ 个正整数 $a_1, a_2, \ldots, a_k$ 的和。

我们将问题分层，第 $i$ 层决定 $a_i$。则为了进行第 $i$ 层决策，我们需要记录三个状态变量：
$n-\sum_{j=1}^i{a_j}$，表示后面所有正整数的和；以及 $a_{i-1}$，表示前一层的正整数，以确保正整数递增；以及 $i$，确保我们最多输出 $m$ 个正整数。

为了记录方案，我们用 $arr$ 数组，第 $i$ 项表示 $a_i$. 注意到 $arr$ 实际上是一个长度为 $i$ 的栈。

int m, arr[103];  // arr 用于记录方案

void dfs(int n, int i, int a) {
  if (n == 0) {
    for (int j = 1; j <= i - 1; ++j) printf("%d ", arr[j]);
    printf("\n");
  }
  if (i <= m) {
    for (int j = a; j <= n; ++j) {
      arr[i] = j;
      dfs(n - j, i + 1, j);  // 请仔细思考该行含义。
    }
  }
}

// 主函数
scanf("%d%d", &n, &m);
dfs(n, 1, 1);

中序遍历

按照访问左子树——根节点——右子树的方式遍历这棵树

方法一：递归

整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程

代码

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();  // 初始化列表
        inorder(root, res);  // 递归返回列表
        return res;
    }

    public void inorder(TreeNode root, List<Integer> res) {  
        if (root == null) {  // 根为空，直接返回
            return;
        }
        inorder(root.left, res);  // 遍历左子树
        res.add(root.val);  // 对根节点处理
        inorder(root.right, res);  // 遍历右子树
    }
}

时间复杂度：$O\left(n\right)$

空间复杂度：$O\left(n\right)$

方法二：迭代

递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来

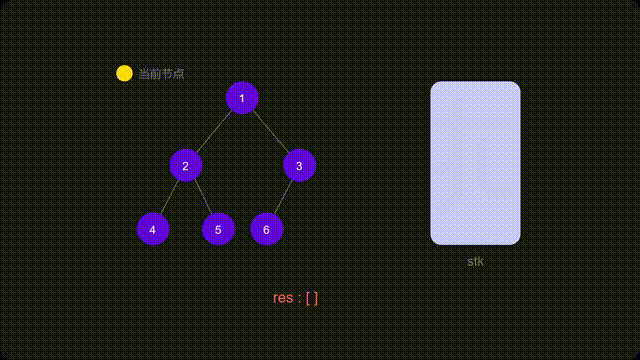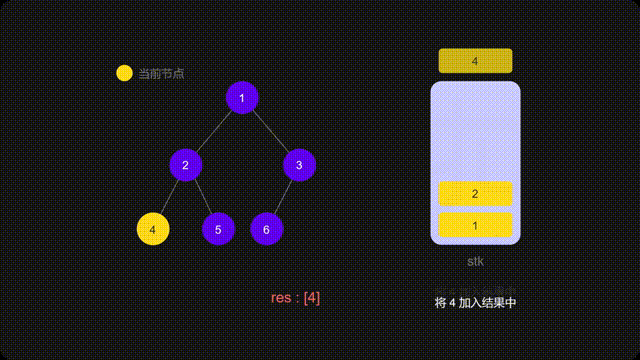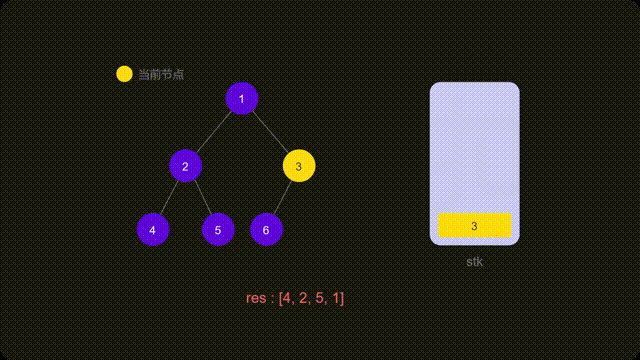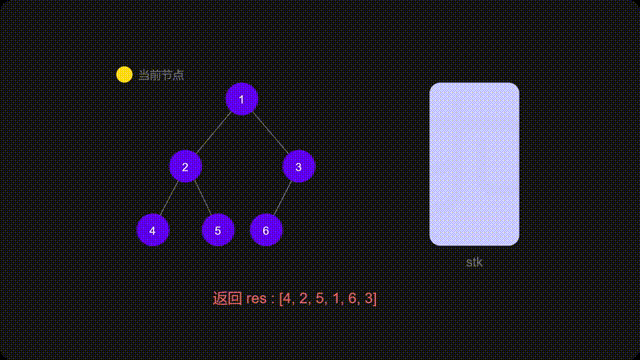
代码

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();  // 初始列表
        Deque<TreeNode> stk = new LinkedList<TreeNode>();  // 初始化栈
        while (root != null || !stk.isEmpty()) {  // 根节点存在，栈不空
            while (root != null) {  // 根节点存在
                stk.push(root);  // 根节点入栈
                root = root.left;  // 前往左节点
            }
            root = stk.pop();  // 根节点出栈
            res.add(root.val);  // 处理根节点
            root = root.right;  // 前往右节点
        }
        return res;
    }
}

时间复杂度：$O\left(n\right)$

空间复杂度：$O\left(n\right)$

方法三：Morris 中序遍历

Morris 遍历算法将非递归的中序遍历空间复杂度降为 $O\left(n\right)$

算法步骤：

• 如果 $x$ 无左孩子：

  1. 先将 $x$ 值加入答案数组
  2. 访问 $x$ 的右孩子，即 $x = x.right$

• 如果 $x$ 有左孩子：找到 $x$ 左子树最右节点 $predecessor$

  • 如果 $predecessor$ 的右孩子为空：
    1. 右孩子指向 $x$
    2. 访问 $x$ 左孩子，即 $x=x.left$
  • 如果 $predecessor$ 的右孩子不为空：
    1. 将 $predecessor$ 置空
    2. $x$ 加入答案数组
    3. 访问 $x$ 右孩子

代码

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();  // 初始化答案数组
        TreeNode predecessor = null;  // 初始化 predecessor
	
        // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
        while (root != null) {  // 根节点不存在
            if (root.left != null) {   // 存在左子树
                predecessor = root.left;  // 前往左节点
                while (predecessor.right != null && predecessor.right != root) {
                    predecessor = predecessor.right;
                }
              
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor.right == null) {
                    predecessor.right = root;
                    root = root.left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    res.add(root.val);
                    predecessor.right = null;
                    root = root.right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                res.add(root.val);
                root = root.right;
            }
        }
        return res;
    }
}

时间复杂度：$O\left(n\right)$

空间复杂的：$O\left(1\right)$

DFS 到叶子

class Solution {
    List<Integer> list = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root) {
        dfs(root);
    }
    public void dfs(TreeNode root){
        if(root == null)  // 根结点为空
            return;
        path();  // 处理路径
        list.add(root.val);  // 
        if(root.left == null && root.right == null)  // 到达叶子
            processLeve;  // 处理叶子节点
        dfs(root.left, num, sum);
        dfs(root.right, num, sum);
        list.remove(list.size() - 1);
    }
}

BFS

BFS 是图论中的一种遍历算法，详见 BFS。

双向搜索

双向同时搜索的基本思路是从状态图上的起点和终点同时开始进行 广搜 或 深搜。

如果发现搜索的两端相遇了，那么可以认为是获得了可行解。

过程

算法的主要思想是将整个搜索过程分成两半，分别搜索，最后将两半的结果合并。

将开始结点和目标结点加入队列 q
标记开始结点为 1
标记目标结点为 2
while (队列 q 不为空)
{
  从 q.front() 扩展出新的 s 个结点

  如果 新扩展出的结点已经被其他数字标记过
    那么 表示搜索的两端碰撞
    那么 循环结束

  如果 新的 s 个结点是从开始结点扩展来的
    那么 将这个 s 个结点标记为 1 并且入队 q 

  如果 新的 s 个结点是从目标结点扩展来的
    那么 将这个 s 个结点标记为 2 并且入队 q
}

适用于输入数据较小，但还没小到能直接使用暴力搜索的情况。

时间复杂度：$O\left(a^{\frac b2}\right)$

启发式搜索

启发式搜索（英文：heuristic search）是一种在普通搜索算法的基础上引入了启发式函数的搜索算法。

启发式函数的作用是基于已有的信息对搜索的每一个分支选择都做估价，进而选择分支。简单来说，启发式搜索就是对取和不取都做分析，从中选取更优解或删去无效解。

A*

A * 搜索算法（英文：A*search algorithm，A * 读作 A-star），简称 A * 算法，是一种在图形平面上，对于有多个节点的路径求出最低通过成本的算法。它属于图遍历（英文：Graph traversal）和最佳优先搜索算法（英文：Best-first search），亦是 BFS 的改进。

过程

定义起点 $s$，终点 $t$，从起点（初始状态）开始的距离函数 $g(x)$，到终点（最终状态）的距离函数 $h(x)$，$h^{\ast}(x)$，以及每个点的估价函数 $f(x)=g(x)+h(x)$。

$A ^*$ 算法每次从优先队列中取出一个 $f$ 最小的元素，然后更新相邻的状态。

如果 $h\leq h*$，则 $A ^*$ 算法能找到最优解。

上述条件下，如果 $h$ 满足三角形不等式，则 $A^ *$ 算法不会将重复结点加入队列。

当 $h=0$ 时，$A^ *$ 算法变为 Dijkstra；当 $h=0$ 并且边权为 $1$ 时变为 BFS。

迭代加深搜索

迭代加深是一种 每次限制搜索深度的 深度优先搜索。

迭代加深搜索的本质还是深度优先搜索，只不过在搜索的同时带上了一个深度 ，当 达到设定的深度时就返回，一般用于找最优解。如果一次搜索没有找到合法的解，就让设定的深度加一，重新从根开始。

既然是为了找最优解，为什么不用 BFS 呢？我们知道 BFS 的基础是一个队列，队列的空间复杂度很大，当状态比较多或者单个状态比较大时，使用队列的 BFS 就显出了劣势。事实上，迭代加深就类似于用 DFS 方式实现的 BFS，它的空间复杂度相对较小。

当搜索树的分支比较多时，每增加一层的搜索复杂度会出现指数级爆炸式增长，这时前面重复进行的部分所带来的复杂度几乎可以忽略，这也就是为什么迭代加深是可以近似看成 BFS 的。

过程

首先设定一个较小的深度作为全局变量，进行 DFS。每进入一次 DFS，将当前深度加一，当发现 d 大于设定的深度 $\textit{limit}$ 就返回。如果在搜索的途中发现了答案就可以回溯，同时在回溯的过程中可以记录路径。如果没有发现答案，就返回到函数入口，增加设定深度，继续搜索。

IDDFS(u,d)
    if d>limit
        return
    else
        for each edge (u,v)
            IDDFS(v,d+1)
return

IDA*

IDA * 为采用了迭代加深算法的 A * 算法。

优点：

由于 IDA * 改成了深度优先的方式，相对于 A * 算法，它的优点如下：

• 不需要判重，不需要排序，利于深度剪枝。
• 空间需求减少：每个深度下实际上是一个深度优先搜索，不过深度有限制，使用 DFS 可以减小空间消耗。

缺点：

• 重复搜索：即使前后两次搜索相差微小，回溯过程中每次深度变大都要再次从头搜索。

实现

Procedure IDA_STAR(StartState)
Begin
  PathLimit := H(StartState) - 1;
  Succes := False;
  Repeat
    inc(PathLimit);
    StartState.g = 0;
    Push(OpenStack, StartState);
    Repeat
      CurrentState := Pop(OpenStack);
      If Solution(CurrentState) then
        Success = True
      Elseif PathLimit >= CurrentState.g + H(CurrentState) then
        For each Child(CurrentState) do
          Push(OpenStack, Child(CurrentState));
    until Success or empty(OpenStack);
  until Success or ResourceLimtsReached;
end;

回溯法

回溯法是一种经常被用在 深度优先搜索（DFS） 和 广度优先搜索（BFS） 的技巧。

其本质是：走不通就回头。

过程

1. 构造空间树；
2. 进行遍历；
3. 如遇到边界条件，即不再向下搜索，转而搜索另一条链；
4. 达到目标条件，输出结果。

Dancing Links

精确覆盖问题是指给定许多集合 $S_i (1 \le i \le n)$ 以及一个集合 $X$，求满足以下条件的无序多元组 $(T_1, T_2, \cdots , T_m)$：

1. $\forall i, j \in [1, m],T_i\bigcap T_j = \varnothing (i \neq j)$
2. $X = \bigcup\limits_{i = 1}^{m}T_i$
3. $\forall i \in[1, m], T_i \in {S_1, S_2, \cdots, S_n}$

问题转化

将 $\bigcup\limits_{i = 1}^{n}S_i$ 中的所有数离散化，可以得到这么一个模型：

给定一个 01 矩阵，你可以选择一些行（row），使得最终每列（column）1都恰好有一个 1。 举个例子，我们对上文中的例子进行建模，可以得到这么一个矩阵：

$$
\begin{pmatrix}
0 & 0 & 1 & 0 & 1 & 1 & 0 \
1 & 0 & 0 & 1 & 0 & 0 & 1 \
0 & 1 & 1 & 0 & 0 & 1 & 0 \
1 & 0 & 0 & 1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 & 0 & 0 & 1 \
0 & 0 & 0 & 1 & 1 & 0 & 1
\end{pmatrix}
$$

其中第 $i$ 行表示着 $S_i$，而这一行的每个数依次表示 $[1 \in S_i],[3 \in S_i],[5 \in S_i],\cdots,[119 \in S_i]$。

Alpha-Beta 剪枝

Minimax 算法

极小化极大算法，是一种找出失败的最大可能性中的最小值的算法。

在局面确定的双人对弈里，常进行对抗搜索，构建一棵每个节点都为一个确定状态的搜索树。奇数层为己方先手，偶数层为对方先手。搜索树上每个叶子节点都会被赋予一个估值，估值越大代表我方赢面越大。我方追求更大的赢面，而对方会设法降低我方的赢面，体现在搜索树上就是，奇数层节点（我方节点）总是会选择赢面最大的子节点状态，而偶数层（对方节点）总是会选择我方赢面最小的的子节点状态。

过程

Minimax 算法的整个过程，会从上到下遍历搜索树，回溯时利用子树信息更新答案，最后得到根节点的值，意义就是我方在双方都采取最优策略下能获得的最大分数。

解释

来看一个简单的例子。

称我方为 MAX，对方为 MIN，图示如下：

例如，对于如下的局势，假设从左往右搜索，根节点的数值为我方赢面：

我方应选择中间的路线。因为，如果选择左边的路线，最差的赢面是 3；如果选择中间的路线，最差的赢面是 15；如果选择右边的路线，最差的赢面是 1。虽然选择右边的路线可能有 22 的赢面，但对方也可能使我方只有 1 的赢面，假设对方会选择使得我方赢面最小的方向走，那么经过权衡，显然选择中间的路线更为稳妥。

实际上，在看右边的路线时，当发现赢面可能为 1 就不必再去看赢面为 12、20、22 的分支了，因为已经可以确定右边的路线不是最好的。

朴素的 Minimax 算法常常需要构建一棵庞大的搜索树，时间和空间复杂度都将不能承受。而 剪枝就是利用搜索树每个节点取值的上下界来对 Minimax 进行剪枝优化的一种方法。

需要注意的是，对于不同的问题，搜索树每个节点上的值有着不同的含义，它可以是估值、分数、赢的概率等等，为方便起见，我们下面统一用分数来称呼。

Alpha-Beta 剪枝

过程

对于如下的局势，假设从左往右搜索：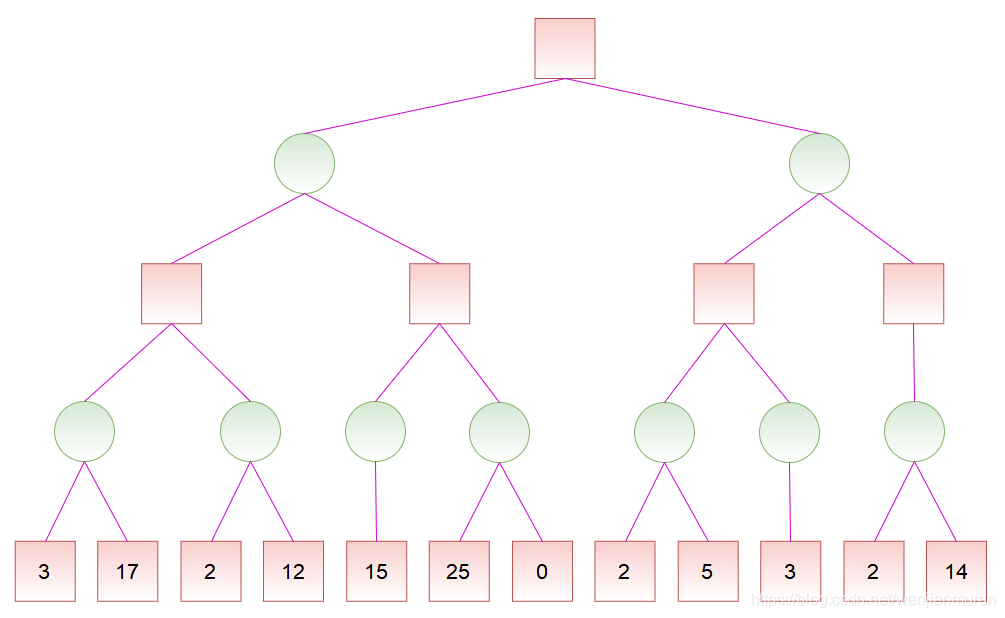

若已知某节点的所有子节点的分数，则可以算出该节点的分数：对于 MAX 节点，取最大分数；对于 MIN 节点，取最小分数。

若已知某节点的部分子节点的分数，虽然不能算出该节点的分数，但可以算出该节点的分数的取值范围。同时，利用该节点的分数的取值范围，在搜素其子节点时，如果已经确定没有更好的走法，就不必再搜索剩余的子节点了。

记 $\mathit{v}$ 为节点的分数，且 $\alpha \leq v \leq \beta$，即 $\alpha$ 为最大下界，$\beta$ 为最小上界。当 $\alpha \geq \beta$ 时，该节点剩余的分支就不必继续搜索了（也就是可以进行剪枝了）。注意，当 $\alpha = \beta$ 时，也可以剪枝，这是因为不会有更好的结果了，但可能有更差的结果。

初始化时，令 $\alpha = -\infty$, $\beta = +\infty$，也就是 $-\infty \leq v \leq +\infty$。到节点 $A$ 时，由于左子节点的分数为 $3$，而节点 $A$ 是 $MIN$ 节点，试图找分数小的走法，于是将 $\beta$ 值修改为 $3$，这是因为 $3$ 小于当前的 $\beta$ 值（$\beta = +\infty$）。然后节点 $A$ 的右子节点的分数为 $17$，此时不修改节点 $A$ 的 $\beta$ 值，这是因为 $17$ 大于当前的 $\beta$ 值（$\beta = 3$）。之后，节点 $A$ 的所有子节点搜索完毕，即可计算出节点 $A$ 的分数为 $3$。

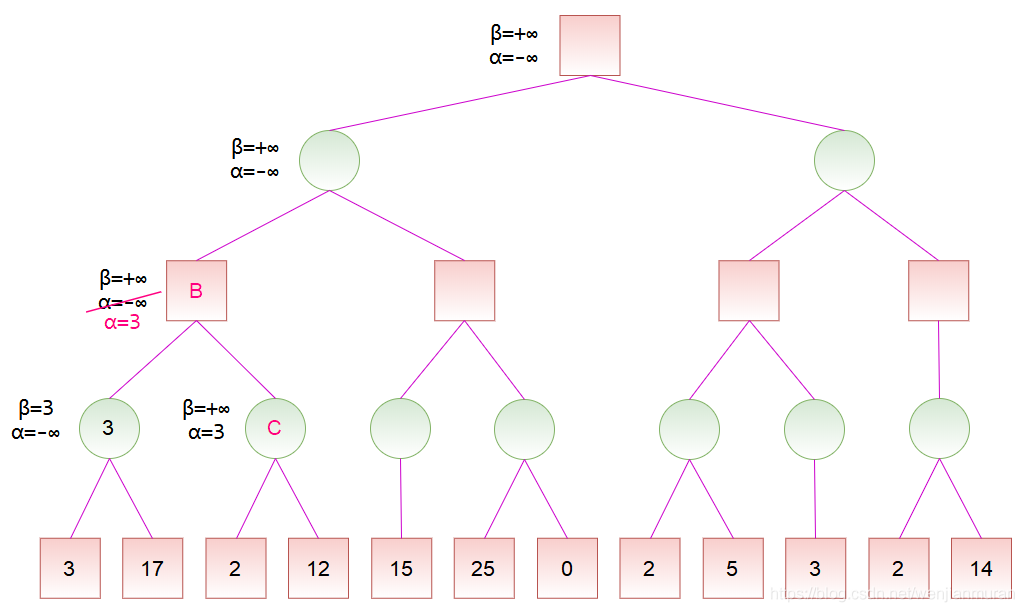
对于节点 C，由于左子节点的分数为 2，而节点 C 是 MIN 节点，于是将 \beta 值修改为 2。此时 \alpha \geq \beta，故节点 C 的剩余子节点就不必搜索了，因为可以确定，通过节点 C 并没有更好的走法。然后，节点 C 是 MIN 节点，将节点 C 的分数设为 \beta，也就是 2。由于节点 B 的所有子节点搜索完毕，即可计算出节点 B 的分数为 3。

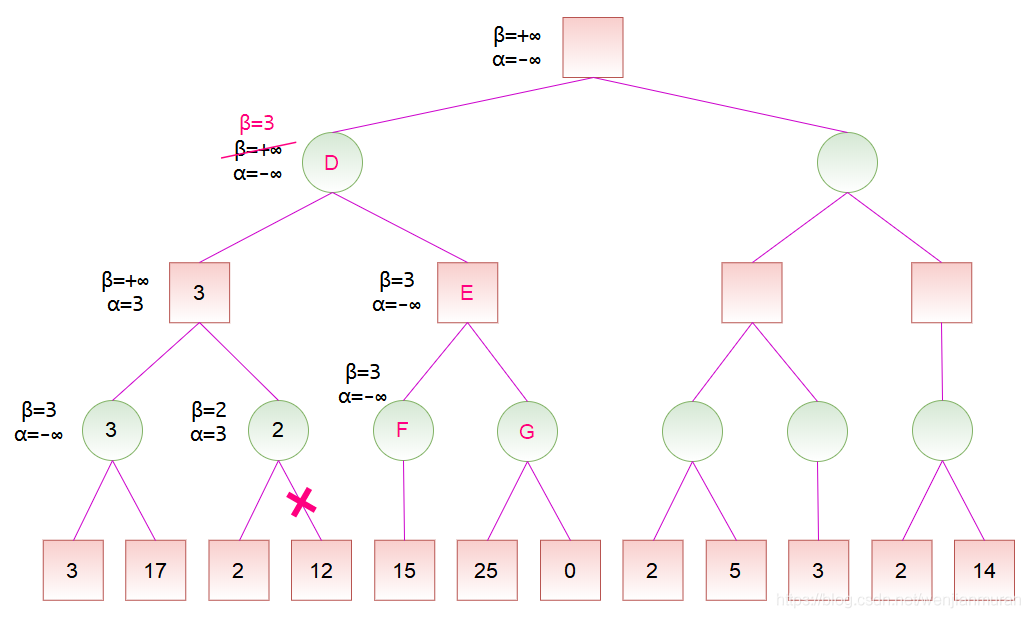
计算出节点 B 的分数后，节点 B 是节点 D 的一个子节点，故可以更新节点 D 的分数范围。由于节点 D 是 MIN 节点，于是将 \beta 值修改为 3。然后节点 D 将 \alpha 和 \beta 值传递给节点 E，节点 E 又传递给节点 F。对于节点 F，它只有一个分数为 15 的子节点，由于 15 大于当前的 \beta 值，而节点 F 为 MIN 节点，所以不更新其 \beta 值，然后可以计算出节点 F 的分数为 15。

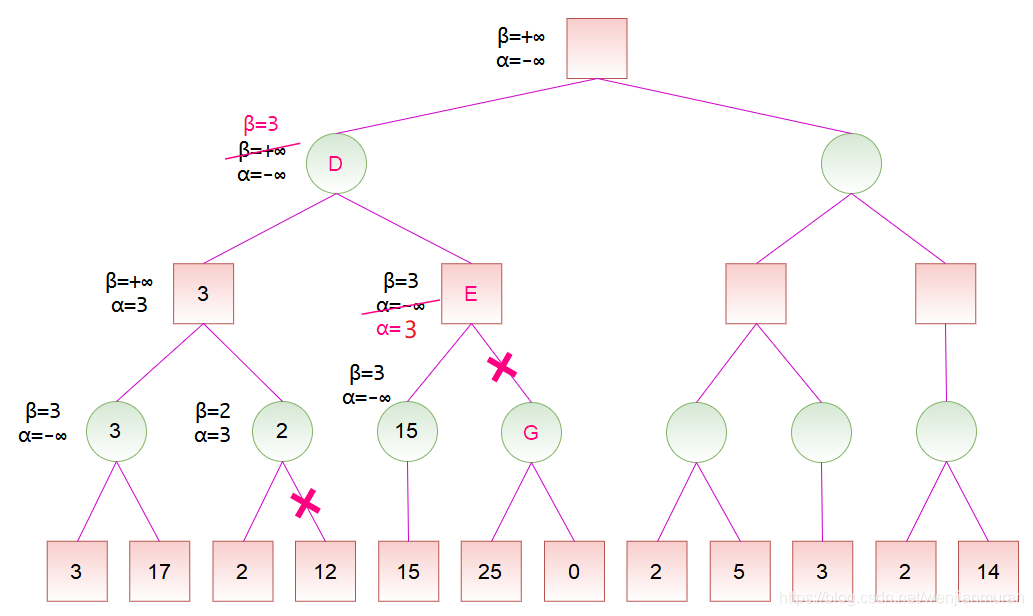
计算出节点 F 的分数后，节点 F 是节点 E 的一个子节点，故可以更新节点 E 的分数范围。节点 E 是 MAX 节点，更新 \alpha，此时 \alpha \geq \beta，故可以剪去节点 E 的余下分支。然后，节点 E 是 MAX 节点，将节点 E 的分数设为 \alpha，也就是 3。此时，节点 D 的所有子节点搜索完毕，即可计算出节点 D 的分数为 3。

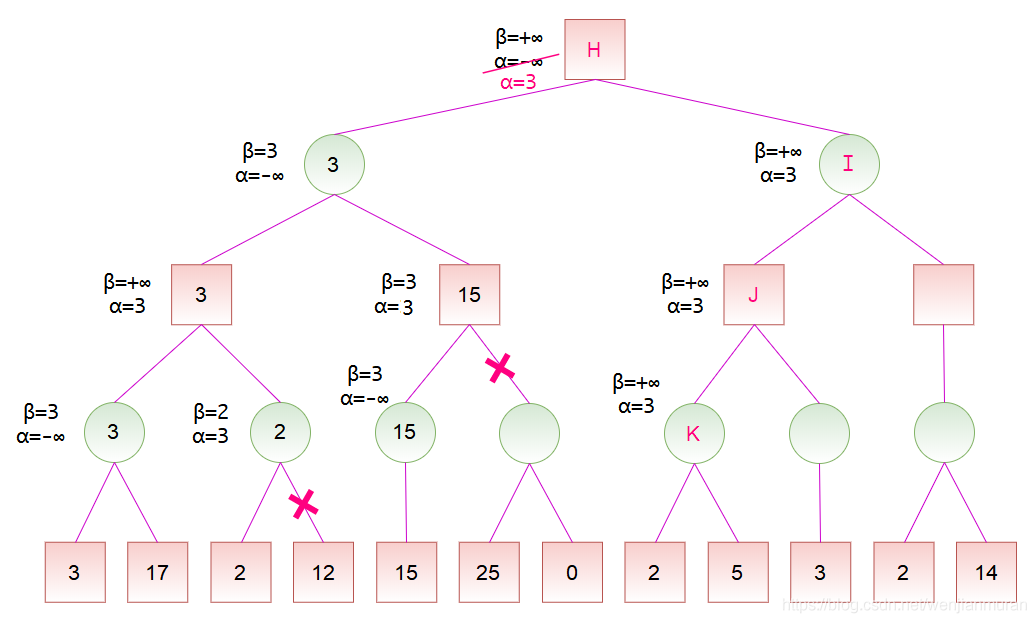
计算出节点 D 的分数后，节点 D 是节点 H 的一个子节点，故可以更新节点 H 的分数范围。节点 H 是 MAX 节点，更新 \alpha。然后，按搜索顺序，将节点 H 的 \alpha 和 \beta 值依次传递给节点 I、J、K。对于节点 K，其左子节点的分数为 2，而节点 K 是 MIN 节点，更新 \beta，此时 \alpha \geq \beta，故可以剪去节点 K 的余下分支。然后，将节点 K 的分数设为 2。

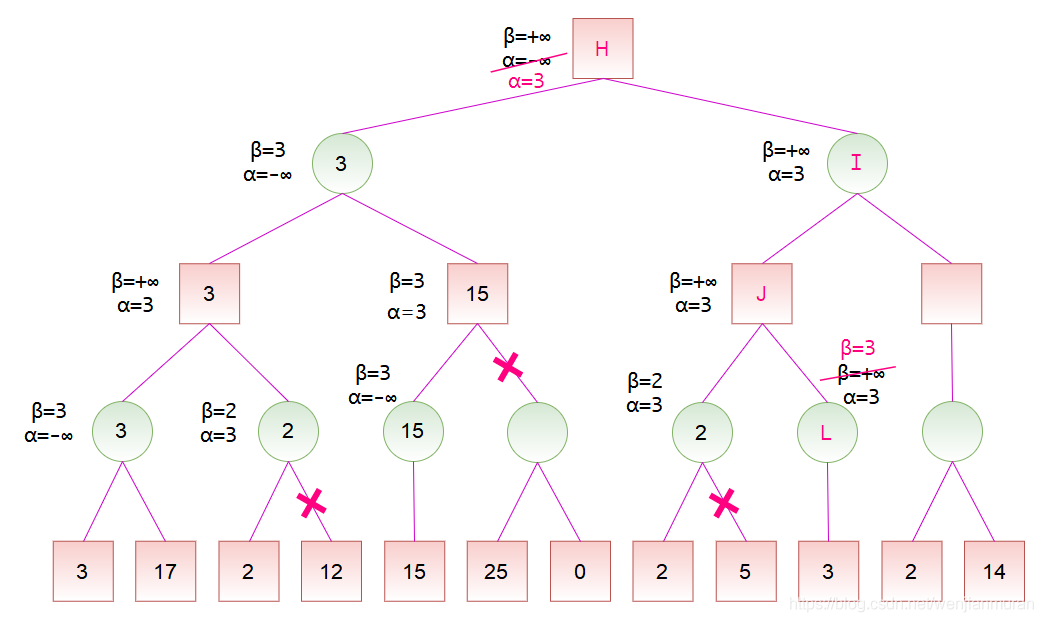
计算出节点 K 的分数后，节点 K 是节点 J 的一个子节点，故可以更新节点 J 的分数范围。节点 J 是 MAX 节点，更新 \alpha，但是，由于节点 K 的分数小于 \alpha，所以节点 J 的 \alpha 值维持 3 保持不变。然后，将节点 J 的 \alpha 和 \beta 值传递给节点 L。由于节点 L 是 MIN 节点，更新 \beta = 3，此时 \alpha \geq \beta，故可以剪去节点 L 的余下分支，由于节点 L 没有余下分支，所以此处并没有实际剪枝。然后，将节点 L 的分数设为 3。

int alpha_beta(int u, int alph, int beta, bool is_max) {
  if (!son_num[u]) return val[u];
  if (is_max) {
    for (int i = 0; i < son_num[u]; ++i) {
      int d = son[u][i];
      alph = max(alph, alpha_beta(d, alph, beta, is_max ^ 1));
      if (alph >= beta) break;
    }
    return alph;
  } else {
    for (int i = 0; i < son_num[u]; ++i) {
      int d = son[u][i];
      beta = min(beta, alpha_beta(d, alph, beta, is_max ^ 1));
      if (alph >= beta) break;
    }
    return beta;
  }
}

优化