数据结构

数据结构是个人觉得 408 中使用的最多的，这是最常用的。

数据结构基本概念

数据结构

• 逻辑结构
• 存储结构
• 数据运算

用抽象数据类型表示：数据对象、数据关系、基本操作集

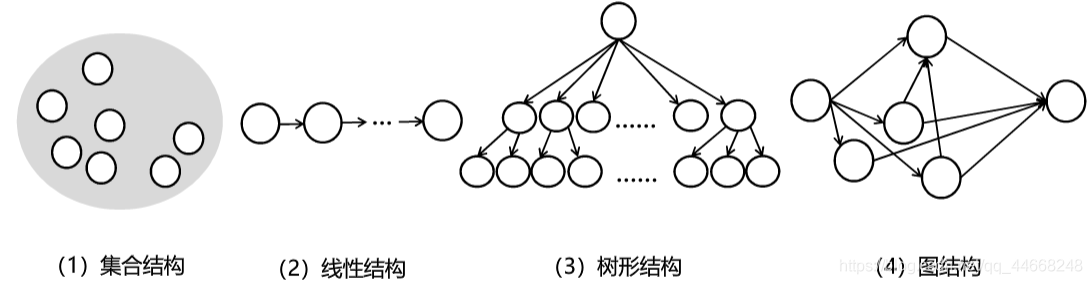
逻辑结构

1. 线性结构 1:1

2. 树形结构 1:n

3. 图结构 m:n

4. 集合结构 没啥关系

存储结构

1. 顺序存储结构 依次存储
2. 链式存储结构 连续的或不连续的存储空间
3. 索引存储 (关键字, 地址)
4. 散列存储 哈希存储

算法复杂度

算法

算法是问题求解步骤的描写

算法特性

1. 有穷性
2. 确定性
3. 可行性
4. 输入
5. 输出

好算法特点

1. 正确性
2. 可读性
3. 健壮性
4. 效率与低存储量需求

算法时间复杂度影响因素

主要因素：问题规模

不影响的因素：

• 描述语言
• 计算机性能

时间复杂度

常见渐近时间复杂度

$O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)$

递归问题时间复杂度

$T(N)=a\times T\left(\dfrac Nb\right)+O\left(N^b\right)$

• $\log\left(b,a\right)>d\rightarrow$复杂度$O\left(N^{\log\left(b,a\right)}\right)$
• $\log\left(b,a\right)=d\rightarrow$复杂度$O\left(N^d\times\log N\right)$
• $\log\left(b,a\right)<d\rightarrow$复杂度$O\left(N^d\right)$

常见的题型

for循环

for(i=0;i<n1;i++)
for(j=0;j<n2;j++)
{
    ...
}

时间复杂度：$O(\prod{n_i})$

do-while循环

do{
    ...
    f(i);
}while(i<=n)

时间复杂度：$\sum{f(i)}=n$的解

do{
    ...
    i++;
}while(i<=n)

时间复杂度：$O(n)$

do{
    ...
    i=k*i;
}while(i<=n)

时间复杂度：$O(log_kn)$

while循环

while(n>=f(y))
{
	...
	y++;
}

时间复杂度：$O(f^{-1}(n))$

空间复杂度

分析除输入和程序之外的额外空间

原地工作：$\text{O}(1)$