考研的高数在正式内容之前,会有一些前置需要掌握的
函数
反函数
$$
x=f^{-1}(y)
$$
反函数导数:
$\dfrac{\text dx}{\text dy}\ =\dfrac{1}{y’}$
$\dfrac{\text d^2x}{\text dy^2}=-\dfrac{y’’_{xx}}{(y’_x)^3}$
$\dfrac{\text{d}^3x}{\text{d}y^3}=\dfrac{3y’’^2-y’y’’’}{y’^5}$
反函数积分:$\int f^{-1}(x)\text dx=xf^{-1}(x)-F(f^{-1}(x))+\text C$
复合函数:$f(f^{-1}(x))=x$
函数性质
有界性:$f(x)$在$(a,b)$内可导且$f’(x)$有界,则$f(x)$在$(a,b)$有界
单调性
奇偶性
常见奇函数:
- $\sin x$、$\tan x$、$\arcsin x$、$ \arctan x$
- $\ln \dfrac{1-x}{1+x}$、
- $ \ln(x+ \sqrt{1+x^2})$
- $\dfrac{e^x-1}{e^x+1}$
- $f(x)-f(-x)$
常见偶函数:
$x^2$
$|x|$
$\cos x$
$\int_{-a}^a|x-t|f(t)\text{d}t$
$f(x)+f(-x)$
$y=f(x)$关于直线$x=A$对称的充要条件是$f(x)=f(2A-x)$或$f(x-A)=f(x+A)$
周期性
常见周期函数
- $f(x)\in T$$\Rightarrow$$\int_a^xf(t)\text{d}t-\dfrac{\int_0^Tf(t)\text{d}t}{T}x$$\in T$
- $x-[x]\in T_{(T=1)}$
导数 & 积分
偶函数求导为奇函数,原函数为奇函数
奇函数求导为偶函数,原函数为偶函数
周期函数的导数依然是周期函数
奇偶性 & 周期性
$f(x)$奇函数$\Rightarrow$$f’(x)$偶函数
$f(x)$偶函数$\Rightarrow$$f’(x)$奇函数
$f(x)$为周期为$T$的周期函数$\Rightarrow$$f’(x)$为周期为$T$的周期函数
$f(x)$为奇函数$\Rightarrow\int_a^x{f\left( t \right)}\text{d}t$偶函数
$f(x)$为偶函数$\Rightarrow$ $\left\{ \begin{array}{l}\int_0^x{f\left( t \right)}\text{d}t\ \text{奇函数}\\\\\int_a^x{f\left( t \right)}\text{d}t\ \ \text{不确定}\\\end{array} \right. $
$f(x)\in T\Rightarrow \int_a^xf(x)\text dx=\left\{ \begin{array}{l} \text{周期函数}\ \ \ \ \ \ \ \int_0^T{f\left( t \right)}\text{d}t\text{收敛}\\\text{非周期函数}\ \ \ \ \int_0^T{f\left( t \right)}\text{d}t\text{发散}\\\end{array}\right. $ $f(x)\in T \Rightarrow$$\int_0^T{f\left( x \right) \text{d}t=\int_a^{a+T}{f\left( x \right) \text{d}t} }$
特殊函数
直角坐标系
绝对值函数
$$
y=\left. | \right. x\left. |\right.
$$
符号函数
$$ \text{sgn} x=\left\{ \begin{array}{l} -1,\ x<0\\ \ 0,\ x=0\\ \ 1,\ x>0\\ \end{array} \right. $$迪利克雷函数
$$ D\left( x \right) =\left\{ \begin{array}{l} 1,\ x\in Q\\ 0,\ x\in R \text{\\} Q \end{array} \right. $$取整函数
$$
y=[x]
$$
极坐标系
心形线
$r=a(1-\cos \theta)=x^2+y^2+ax=a\sqrt{x^2+y^2}$
图像
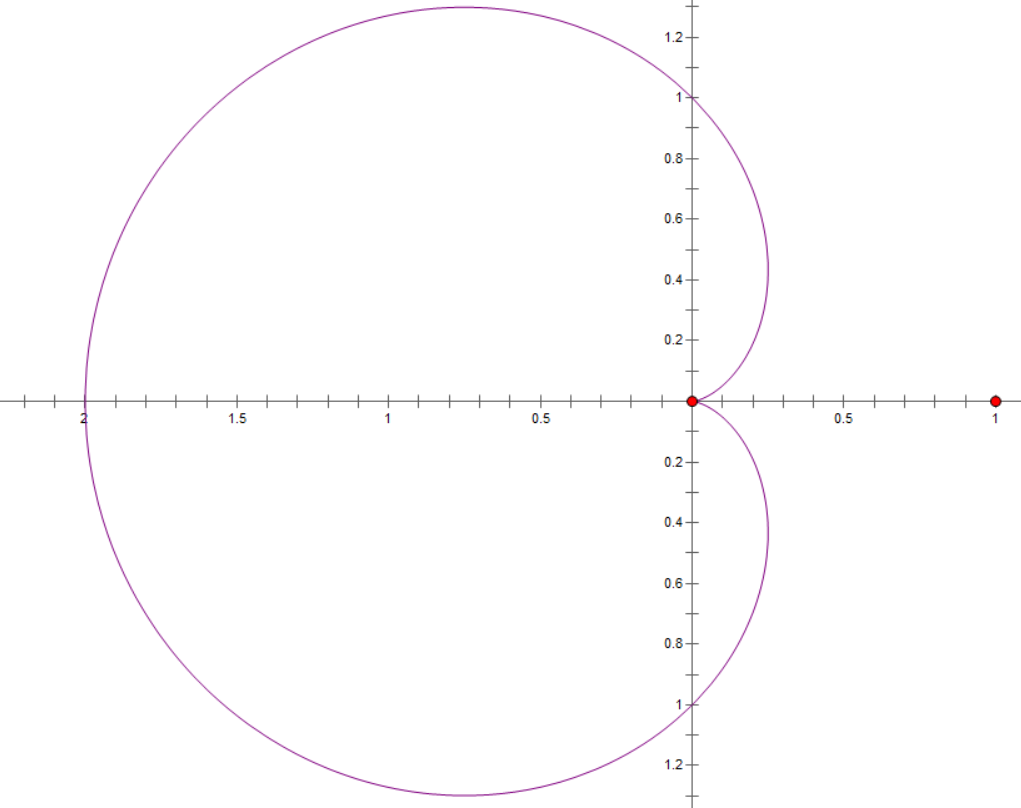
参数
| $\theta$ | $0$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ | $\dfrac{2\pi}{3}$ | $\dfrac{3\pi}{4}$ | $\dfrac{5\pi}{6}$ | $\pi$ |
|---|---|---|---|---|---|---|---|---|---|
| $r$ | $0$ | $\dfrac{2-\sqrt{3}}{2}a$ | $\dfrac{2-\sqrt{2}}{2}a$ | $\dfrac{1}{2}a$ | $a$ | $\dfrac{3}{2}a$ | $\dfrac{2+\sqrt{2}}{2}a$ | $\dfrac{2+\sqrt{3}}{2}a$ | $2a$ |
面积:$\dfrac32\pi a^2$
弧长:$8a$
玫瑰线
公式:$r=a\sin (k\theta)$
图像
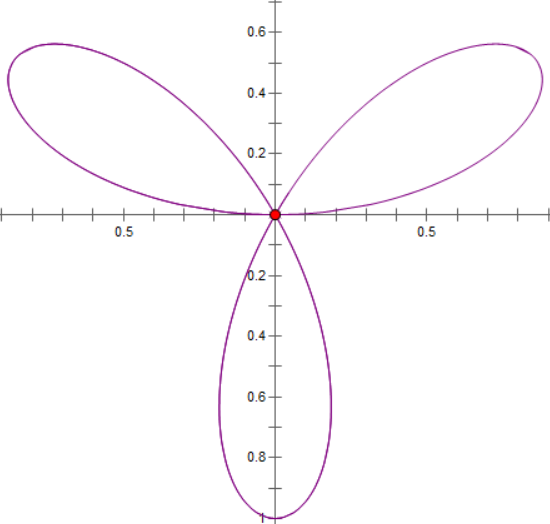
参数
| $\theta$ | $0$ | $\dfrac{\pi}{12}$ | $ \dfrac{\pi}{6}$ | $ \dfrac{\pi}{4}$ | $ \dfrac{\pi}{3}$ | $\dfrac{5\pi}{12}$ | $ \dfrac{\pi}{2}$ | $\dfrac{7\pi}{12}$ | $ \dfrac{2\pi}{3}$ |
|---|---|---|---|---|---|---|---|---|---|
| $r$ | $0$ | $\dfrac{\sqrt{2}}{2}a$ | $a$ | $\dfrac{\sqrt{2}}{2}a$ | $0$ | $-\dfrac{\sqrt{2}}{2}a$ | $-a$ | $-\dfrac{\sqrt{2}}{2}a$ | $0$ |
面积:$S=\left\{ \begin{array}{l} \dfrac{\pi a^2}{2}\ \ k\text{为偶数}\\ \dfrac{\pi a^2}{4}\ \ k\text{为奇数}\\\end{array} \right. $
阿基米德螺旋线
公式:$r=a\theta$
图像
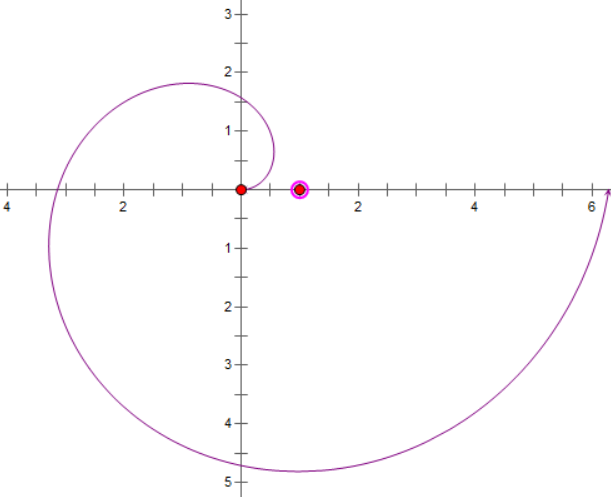
伯努利双纽线
公式:$(x^2+y^2)^2=2a^2(x^2-y^2)\\ r^2=a^2\cos 2\theta\\ r^2=a^2\sin 2\theta\\$
图像
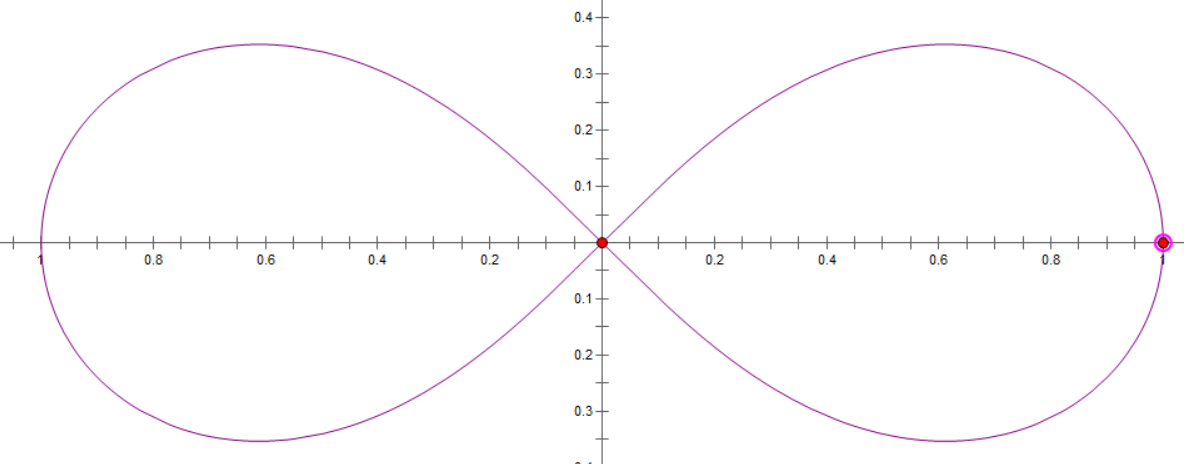
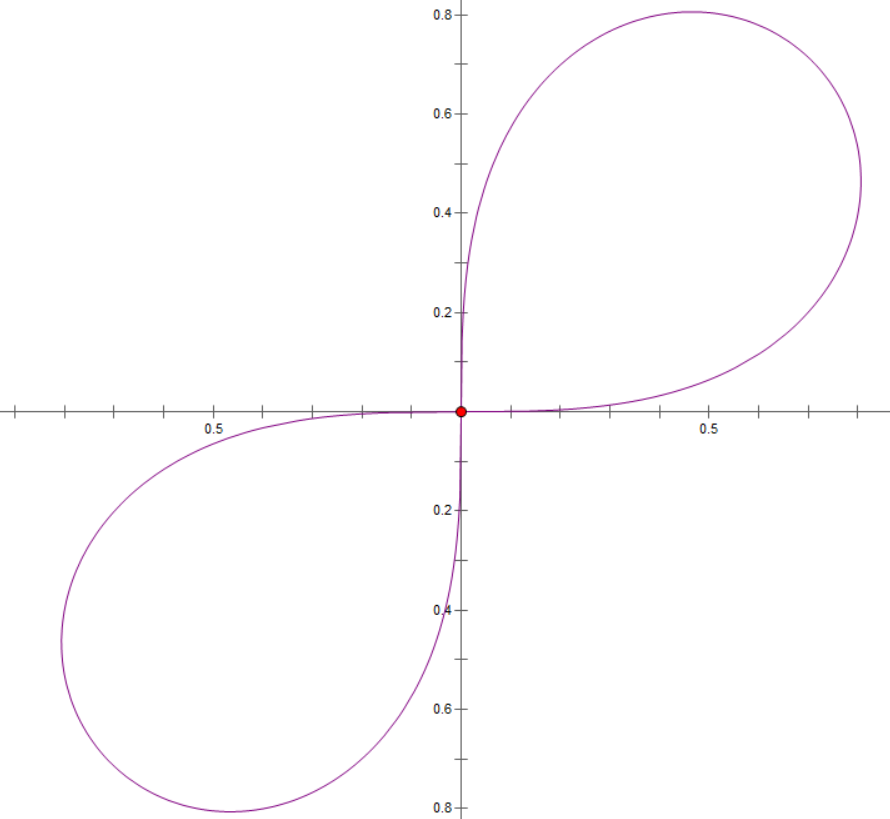
面积:$1$
参数方程下图像
摆线
公式:$\left\{ \begin{array}{l} x=r\left( t-\sin t \right)\\ y=r\left( 1-\cos t \right)\\ \end{array} \right.$
图像
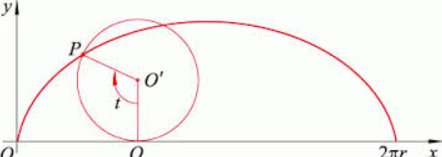
面积:$3\pi r^2$
弧长:$8r$
星形线
公式:$\left\{ \begin{array}{l} x=r\left.\cos^3t \right.\\ y=r\left.\sin^3t \right.\\ \end{array} \right.\\ x^\frac{2}{3}+y^\frac{2}{3}=r^\frac{2}{3}$
图像
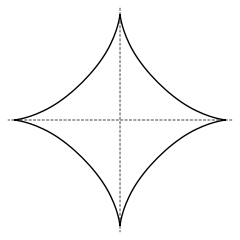
面积:$\dfrac 38\pi r^2$
弧长:$6r$
gama函数
$\varGamma $函数:$\Gamma(n)$$=\int_0^{+\infty}t^{n-1}\text e^{-t}\text dt\\=2\int_0^{+\infty}t^{2n-1}\text e^{-t^2}\text dt\\=(n-1)!$
$B$函数:$B(m,n)=\int_0^1x^{m-1}(1-x)^{n-1}\text dx=\dfrac{\Gamma(m)\Gamma(n)}{\Gamma(m+n)}$
性质
$\Gamma(n+1)=n\Gamma(n)$
$\Gamma(0)=1$
$\Gamma(1)=1$
$\Gamma(\dfrac12)=\sqrt\pi$
余元公式:$\varGamma \left( n \right) \Gamma \left( 1-n \right) =\dfrac{\pi}{\sin \left( n\pi \right)} \\ \Gamma \left( \dfrac{1}{2}-n \right) \Gamma \left( \dfrac{1}{2}+n \right) =\dfrac{\pi}{\cos \left( n\pi \right)}$
数列
等差数列
通项公式:$a_n=a_1+(n-1)d$
求和公式:$S_n$$=\dfrac{n}{2}(a_1+a_n)\=\dfrac{n}{2}[2a_1+(n-1)d]$
等比数列
通项公式:$a_n=a_1q^{n-1}$
求和公式:$S_n=\dfrac{a_1(1-q^n)}{1-q}(q≠1)$
常见求和
- $\sum k =\dfrac{n(n+1)}{2}$
- $\sum k^2=\dfrac{n(n+1)(2n+1)}{6}$
- $\sum k^3=(\dfrac{n(n+1)}2)^2$
- $\sum \dfrac{1}{k(k+1)}=\dfrac{n}{n+1}=1-\dfrac1{n+1}$
- $\sum \dfrac{1}{k^2}=2-\dfrac{1}{k}$
三角函数
基本关系
$\csc x=\dfrac{1}{\sin x}$
$\sec x=\dfrac{1}{\cos x}$
$\cot x=\dfrac{1}{\tan x}$
$\sin^2x+\cos^2x=1$
$1+\tan^2x=\sec^2x$
$1+\cot^2x=\csc^2x$
倍角公式
- $\sin 2x=2\sin x\cos x$
- $\cos 2x=\cos^2x-\sin^2x=2\cos^2x-1=1-2\sin^2x$
- $\tan 2x=\dfrac{2\tan x}{1-\tan^2 x}$
- $\cot 2x=\dfrac{\cot^2x-1}{2\cot x}$
- $\sin 3x=-4\sin^3x+3\sin x$
- $\cos 3x=4\cos^3 x-3\cos x$
半角公式
- $\sin \dfrac{x}{2}=±\sqrt{\dfrac{1-\cos x}{2}}$
- $\cos \dfrac{x}{2}=±\sqrt{\dfrac{1+\cos x}{2}}$
- $\tan \dfrac{x}{2}=\dfrac{1-\cos x}{\sin x}=\dfrac{\sin x}{1+\cos x}=±\sqrt{\dfrac{1-\cos x}{1+\cos x}}$
- $\cot \dfrac{x}{2}=\dfrac{1+\cos x}{\sin x}=\dfrac{\sin x}{1-\cos x}=±\sqrt{\dfrac{1+\cos x}{1-\cos x}}$
积化和差
- $\sin \alpha \cos \beta =\dfrac{1}{2}\left[ \sin \left( \alpha +\beta \right) +\sin \left( \alpha -\beta \right) \right] $
- $\cos \alpha \sin \beta =\dfrac{1}{2}\left[ \sin \left( \alpha +\beta \right) -\sin \left( \alpha -\beta \right) \right] $
- $\cos \alpha \cos \beta =\dfrac{1}{2}\left[ \cos \left( \alpha +\beta \right) +\cos \left( \alpha -\beta \right) \right] $
- $\sin \alpha \sin \beta =\dfrac{1}{2}\left[ \cos \left( \alpha -\beta \right) -\cos \left( \alpha +\beta \right) \right] $
和差化积
- $\sin \alpha +\sin \beta =2\sin \dfrac{\alpha +\beta}{2}\cos \dfrac{\alpha -\beta}{2}$
- $\sin \alpha -\sin \beta =2\sin \dfrac{\alpha -\beta}{2}\cos \dfrac{\alpha +\beta}{2}$
- $\cos \alpha +\cos \beta =2\cos \dfrac{\alpha +\beta}{2}\cos\dfrac{\alpha -\beta}{2}$
- $\cos \alpha -\cos \beta =-2\sin \dfrac{\alpha +\beta}{2}\sin \dfrac{\alpha -\beta}{2}$
万能公式
令$\alpha=\tan \dfrac{x}{2}$
- $\sin x=\dfrac{2\alpha}{1+\alpha^2}$
- $\cos x =\dfrac{1-\alpha^2}{1+\alpha^2}$
因式分解
- $(a+b)^3=a^3+3a^2b+3ab^2+b^3$
- $(a-b)^3=a^3-3ab^2+3ab^2-b^3$
- $a^3-b^3=(a-b)(a^2+ab+b^2)$
- $a^3+b^3=(a+b)(a^2-ab+b^2)$
- $a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+…ab^{n-2}+b^{n-1})$
- $a^n+b^n=(a-b)(a^{n-1}+a^{n-2}b+…ab^{n-2}+b^{n-1})$
不等式
$|a±b|\le|a|+|b|$
$||a|-|b||\le|a-b|$
$|\int f(x)dx|\le\int|f(x)|dx$
$\sqrt{ab}\le\dfrac{a+b}{2}\le\sqrt{\dfrac{a^2+b^2}{2}}$
$\sqrt[3]{abc}\le\dfrac{a+b+c}{3}\le\sqrt{\dfrac{a^2+b^2+c^3}{3}}$
$\sin x<x<\tan x$
$\arctan x\le x\le \arcsin x$
$e^x\ge x+1$
$\dfrac{1}{1+x}<\ln(1+\dfrac{1}{x})<\dfrac{1}{x}$
$x-\dfrac{x^2}2<\ln(1+x)<x$
$x-\dfrac{x^3}6<\sin x<x$
$[x]\le x$
$[x+m]=[x]+m$,其中$m$为整数
Theorem不等式
$\left. \begin{array}{r} f\left( x \right) \in \text{C}_{\left[ a,b \right]}\\ f\left( a \right) =f\left( b \right) =0\\ \end{array} \right\}\\ \Rightarrow \int_a^b{|f\left( x \right) |^2}\text{d}x\le \dfrac{\left( b-a \right) ^2}{\pi}\int_a^b{|f^2\left( x \right) |}'\text{d}x$
复分析
留数定理
$\dfrac1{(x+m)(x+n)^2}=\dfrac A{x+m}+\dfrac B{x+n}+\dfrac C{(x+n)^2}$


