排序

算法 数据结构
算法
发布日期:   2022-03-07
更新日期:   2024-12-20

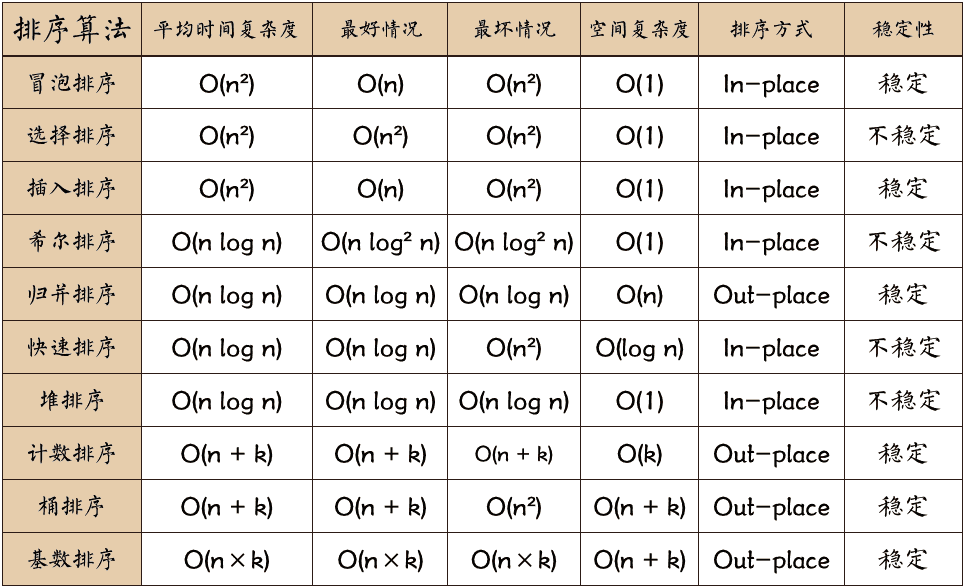
内部排序

插入排序

直接插入排序

某一过程的状态

有序序列L(i)无序序列

特征：前部分有序

算法步骤

  1. 前$i$元素组成有序区

    后$n-i-1$个元素组成无序区

  2. 将第$i$个元素按序插入有序区

  3. 以此类推

插入排序

代码

void InsertSort(List L){
    for(int i = 2; i <= n; ++i){
        if(L[i] < L[i-1]){
            L[0] = L[i];
            for(int j = i - 1; L[0] < L[j]; --j)
                L[j+1] = L[j];
            L[j+1] = L[0];
        }
    }
}

算法性能

  • 空间效率：$\text{O}(1)$
  • 时间效率：
    • 最好情况：$\text{O}(n)$
    • 最坏情况：移动$\sum_{i=2}^n(i+1)$
    • 平均情况：$\text{O}(n^2)$
  • 稳定性：√
  • 适用性：基本有序顺序表

折半插入排序

代码

void InsertSort(ElemType A[], int n){
	int low, high, mid;
	for(int i=0 ; i <= n ; i++){
		A[0] = A[i];  // A[i]暂存A[0] 折半查找 
		low = 1; high = i-1;
		while(low <= high){  // 
			mid = (low + high) / 2;
			if(A[mid] > A[0])
				high = mid - 1;
			else
				low = mid + 1;
		}
		for(int j = i-1; j >= high + 1; --j){  // 统一后移 
			A[j+1] = A[j];
		A[high+1] = A[0];
		}
	}
}

算法性能

减少了比较次数$\text{O}(n\log n)$

  • 时间效率：$\text{O}(n^2)$
  • 适用性：数据率不大的排序表

希尔排序

void ShellSort(ElemType A[], int n){
	for(int dk = n / 2; dk >= 1; dk = dk / 2)  // 步长从一半逐渐减少 
		for(int i = dk + 1; i <= n; ++i)  // 步长右移 
			if(A[i] < A[i - dk]){
				A[0] = A[i];
				for(int j = i-dk; j>0 && A[0]<A[j]; j -= dk)
					A[j+dk] = A[j];
				A[j+dk] = A[0];
			}
}

算法性能

  • 空间效率：$\text{O}(1)$
  • 时间效率：$\text{O}(n^2)$
  • 稳定性：×
  • 适用性：顺序存储线性表

交换排序

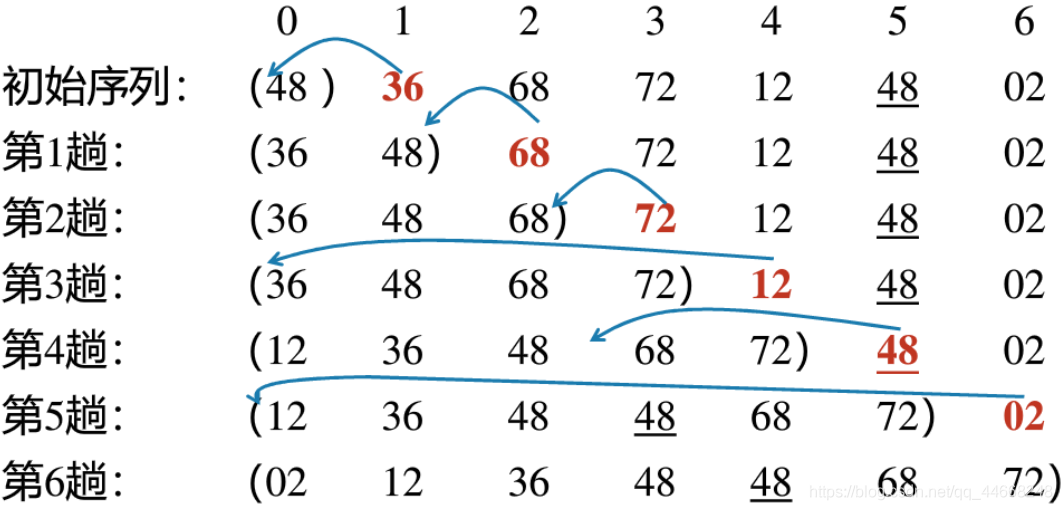
冒泡排序

算法步骤

  1. 检查$D[0],D[1]$，$D[1],D[2]$，$……$，$D[n-i-1],D[n-i]$是否逆序，逆序则交换

冒泡排序

代码

void BubbleSort(List *list)
{
    int i,j; // i标识每趟排序范围最后一个元素下标，每趟排序下标为0~i
    BOOL isSwap = FALSE; // 标记一趟排序中是否发生了元素交换
    for(i = list->n-1 ; i > 0 ; i--)
        for(j = 0 ; j < i ; j++)
            if(list->D[j].key > list->D[j+1].key)
            {
                Swap(list->D, j, j+1);
                isSwap = TRUE;
            }
    if(!isSwap) // 若本趟排序无元素交换，排序完成
        break;
}

算法性能

  • 空间效率：$\text{O}(1)$
  • 时间效率：
    • 比较次数：$\dfrac{n(n-1)}{2}$
    • 移动次数：$\dfrac{3n(n-1)}{2}$
    • 最坏情况：移动$\sum_{i=2}^n(i+1)$
    • 平均情况：$\text{O}(n^2)$
  • 稳定性：√
  • 适用性：顺序存储线性表

快速排序

特征：第$i$躺有$i$个元素到达最终位置

步骤

  1. 待排序序列元素数量小于1，退出

  2. 选择分割元素$D_s$，划分为左右子序列

    左子序列所有元素小于$D_s$

    右子序列所有元素大于$D_s$

  3. 子序列快速排序

快速排序

代码

int Partition(List *list, int low, int high)
{
    int i = low;
    int j = high+1;
    Entry pivot = list->D[low]; // pivot是分割元素
    do{
        do
            i++;
        while(list->D[i].key < pivot.key && i <= high); // i前进
        do
            j--;
        while(list->D[i].key > pivot.key && j >= low); // i前进
        if(i < j)
            Swap(list->D, i, j);
    }while(i < j);
    Swap(list->D, low, j);
    return j; // j是分割元素下标
}

算法性能

  • 空间效率：调用递归工作栈
    • 最好情况：$\text{O}(\log n)$
    • 最坏情况：移动$\text{O}(n)$
    • 平均情况：$\text{O}(\log n)$
  • 时间效率：
    • 平均情况：$\text{O}(\log n)$
  • 稳定性：×
  • 适用性：顺序存储线性表

选择排序

简单选择排序

void SelectSort(List* list)
{
    int minIndex,startIndex = 0;
    while(startIndex < list->n-1)
    {
        minIndex = FindMin(*list, startIndex);
        Swap(list->D, startIndex, minIndex);
        startIndex++;
    }
}
  • 空间效率：$\text{O}(1)$
  • 时间效率：$\text{O}(n^2)$
  • 稳定性：×

堆排序

步骤

交换堆顶元素$D[0]$与堆底元素$D[n-i]$，调整为最大堆

堆排序

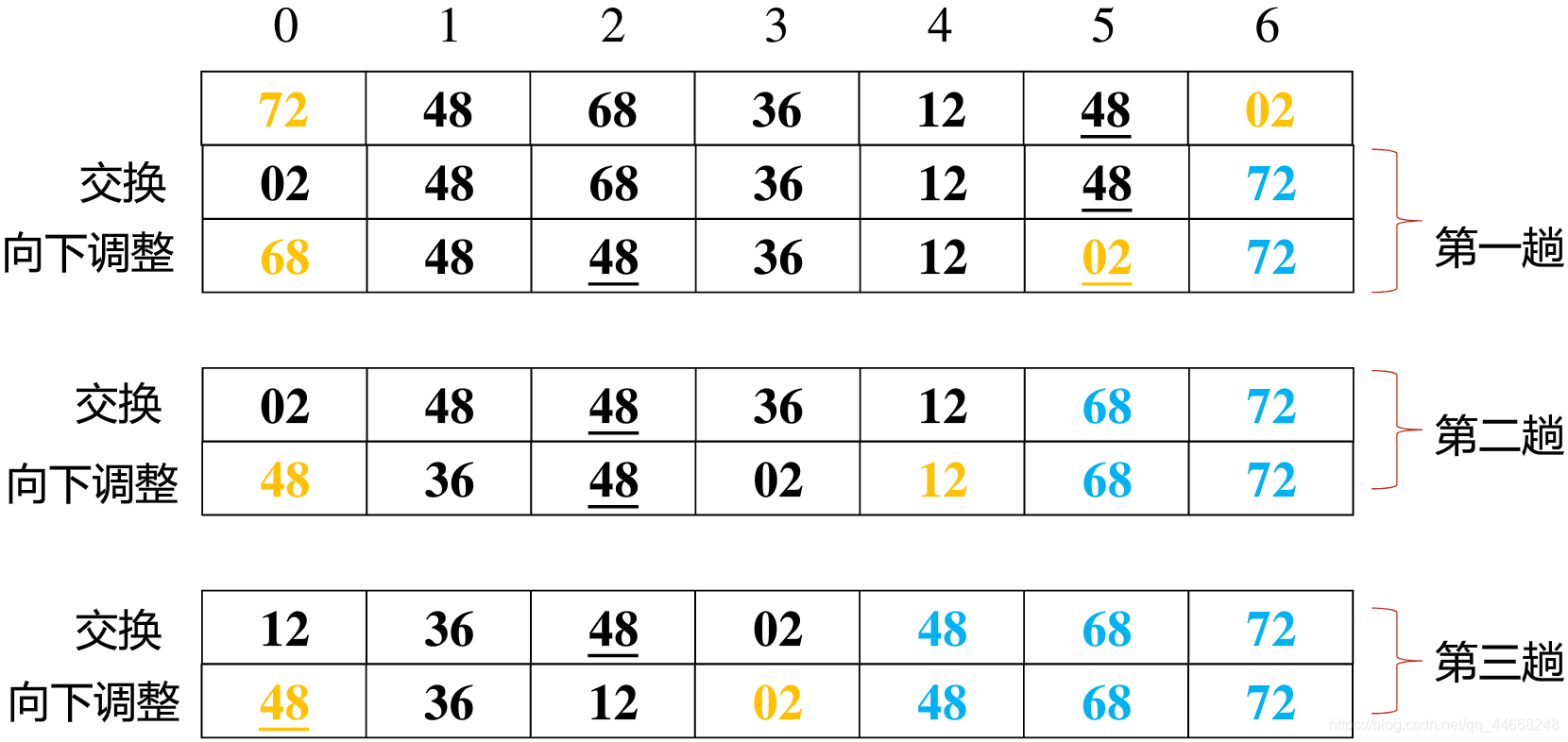
算法性能

  • 空间效率：$\text{O}(1)$
  • 时间效率：
    • 最好情况：$\text{O}(n\log n)$
    • 最坏情况：$\text{O}(n\log n)$
    • 平均情况：$\text{O}(n\log n)$
  • 稳定性：×

归并排序 & 基数排序

归并排序

将两个有序序列合并成一个有序序列则是利用了经典的「归并排序」。

比较次数：$\left[N,2N-1\right]$

步骤

对$[\dfrac{n}{2^{i-1}}]$个有序序列，合并$(D[0],…,D[2^{i-1}-1])$和$(D[2^{i-1}],…,D[2^{i}-1])$

  • 若$[\dfrac{n}{2^{i-1}}]$是偶数，合并最后两个有序序列，否则最后一个序列不合并

代码

/*子序列合并*/
void Merge(List *list, Entry *temp, int low, int n1, int n2)
{
    int i =low, j = low + n1; // i,j初始时分别指向两个序列第一个元素
    while( i <= low + n1 -1 && j <= low + n1 + n2 -1)
    {
        if(list->D[i].key <= list->D[j].key)
            *temp++ = list->D[i++];
        else
            *temp++ = list->D[j++];
    }
    while(i <= low + n1 - 1)
        *temp++ = list->D[i++]; // 剩余元素直接拷贝至temp
    while(j <= low + n1 + n2 -1)
        *temp++ = list->D[j++]; // 剩余元素直接拷贝至temp
}

void MergeSort(List *list)
{
    Entry temp[MaxSize];
    int low, n1, n2, i, size = 1;
    while(size < list->n)
    {
        low = 0; // low是一对待合并序列第一个序列第一个下标
        while(low + size < list->n) // 至少两个序列要合并
        {
            n1 = size;
            if(low + size*2 < list->n)
                n2 = size; // 计算第二个序列长度
            else
                n2 = list->n - low -size;
            Merge(list, temp+low, low, n1, n2);
            low += n1 + n2; // 确定下一对待合并序列中第一个序列第一个元素下标
        }
        for(i=0 ; i<low ; i++)
            list->D[i] = temp[i]; // 复制一趟合并排序结果
        size *= 2; // 子序列长度翻倍
    }
}

算法性能

  • 空间效率：$\text{O}(n)$
  • 时间效率：
    • 平均情况：$\text{O}(n\log n)$
  • 稳定性：√

基数排序

算法性能

  • 空间效率：$\text{O}(r)$
  • 时间效率：
    • 平均情况：$\text{O}(d(n+r))$
  • 稳定性：×

外部排序

特点：

  • 文件较大，内存放不下
  • 算法：归并排序
  • 减少内外存读取次数：增大归并路数败者树、减少归并段数置换选择排序

初始归并段个数：$r=$磁盘记录$/$内存工作区容量

归并趟数：$S=\left\lceil\log_mr\right\rceil$

不使用败者树比较次数：$S(n-1)(m-1)=\left\lceil\log_mr\right\rceil(n-1)(m-1)$

使用败者树比较次数：$S(n-1)\left\lceil\log_mr\right\rceil=(n-1)=\left\lceil\log_2r\right\rceil$

缓冲：$m$个输入缓冲区；$1$个输出缓冲区

总结

关键字比较次数：$\left \lceil \log_2(n!) \right \rceil \le t \le \dfrac{n(n-1)}2$

排序算法比较

趟数和初始状态有关：交换类、直接插入排序$n-1$、简单排序$n-1$、基数排序$d$

复杂度 插入 折半 希尔 冒泡 快速 选择 堆 归并 基数
最好 $O(n)$ $O(n)$ $O(n)$ $O(\log n )$ $O(n^2)$ $O(n\log n )$ $O(n\log n )$ $
最差 $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(n\log n )$ $O(n\log n )$ $
平均 $O(n^2)$ $O(n^2)$ $O(n^{1.3})$ $O(n^2)$ $O(n\log n )$ $O(n^2)$ $O(n\log n )$ $O(n\log n )$ $

空间复杂度

插入排序 插入排序 希尔排序 冒泡排序 快速排序 选择排序 堆排序 归并排序 基数排序
$O(1 )$ $O(1)$ $O(1 )$ $O(1 )$ $O(\log n )$ $O(1 )$ $O(1 )$ $O(n)$ $

稳定性

插入排序 希尔排序 冒泡排序 快速排序 选择排序 堆排序 归并排序 基数排序
√ × √ × × × √ √

一趟确定位置

插入排序 希尔排序 冒泡排序 快速排序 选择排序 堆排序 归并排序 基数排序
× × √ √ √ √ ×

适用场合

插入排序 希尔排序 冒泡排序 快速排序 选择排序 堆排序 归并排序 基数排序
基本有序递增 基本有序且简单快速实现 非常无序 无 关键字较多；取排序前$k$个元素 多数场合，不要节省空间外部排序 不可对浮点数排序

文章作者: Jarrycow
文章链接: http://jarrycow.top/posts/sort.html
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Jarrycow !
算法 数据结构
赏
评论
  目录