堆栈和队列

堆栈和队列是对进出关系限制的线性表。

[toc]

栈堆

存储方式

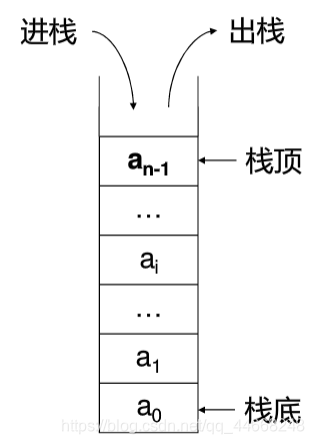
• 后进先出

  共有$\dfrac{C^n_{2n}}{n+1}$种出栈顺序

顺序栈

定义

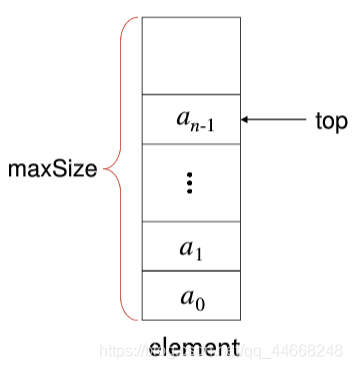
typedef struct{
    int top; // 栈顶位置下标
    int maxSize; // 栈最大容量
    ElemType *data; //栈数组首地址
}SqStack

• 栈顶：S.top
• 空栈：S.top = -1
• 满栈：S.top == MaxSize-1
• 栈长：S.top + 1

创建空堆栈

void InitStack(SqStack *S, int mSize){ //S:栈地址 mSize:最大容量
	S->maxSize = mSize; //获取最大容量
	S->data = (ElemType*)malloc(sizeof(ElemType)*mSize); //给栈申请空间
	S->top=-1; //栈顶为负
}

销毁且释放空间

void Destroy(SqStack *S)
{
    S->maxSize = -1; //容量为负
    free(S->data); //释放栈数组
    S->top = -1; //栈顶为负
}

销毁但不释放

void Clear(SqStack *S)
{
    S->top = -1; //仅仅将栈顶归负
}

取栈顶元素

bool Top(SqStack *S, ElemType *x){
    if(StackEmpty(S)) //空栈
        return ERROR；
    *x = S->data[S->top]; //取栈顶
    return TRUE;
}

入栈

bool Push(SqStack *S, ElemType x){
    if(StackFull(S)) // 溢出
        return FALSE;
    S->top++; //栈顶上移
    S->data[S->top] = x; //栈顶取值
    return TRUE;
}

出栈

bool Pop(SqStack *S, ElemType *x){
    if(IsEmpty(S)) //空栈
        return TRUE;
    x = S->data[S->top];  // 出栈
    S->top--; //栈顶下移
    return TRUE;
}

• 满栈——S->top == S->maxSize-1
• 空栈——S->top == -1

共享栈

两个顺序栈共享一个一维数组

• $0$号栈空：top0 = -1

  $1$号栈空：top1 = MaxSize

• 满栈：top1 - top0 = 1

• $0$号栈进栈：S[++top0] = x;

  $1$号栈进栈：S[--top1] = x;

• $0$号栈出栈：x = S[top0--];

  $1$号栈出栈：x = S[top1++];

链接表示代码

定义

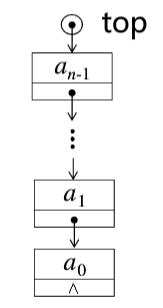
typedef struct node{
    ElemType data; //栈元素数据域
    struct Node* link; //栈元素指针域
}Node;
typedef struct LiStack
{
    Node *top; //栈顶地址
}LiStack;

进栈

void Push(LiStack *S, ElemType x)
{
    Node *p = (Node*)malloc(sizeof(Node)); //给结点申请空间
    p->data = x; // 结点赋值
    p->link = NULL; // 结点指针指向空
    p->link = S->top; // 结点指向栈顶元素
    S->top = p; // 结点变为栈顶
}

出栈

void Pop(LiStack *S)
{
    if(S->top == NULL) // 空栈
        return;
    Node *p = S->top; // 结点为栈顶
    S-top = p->link; //栈顶取结点所指向
    free(p); // 释放结点
}

队列

存储方式

typedef struct{
	ElemType data[MaxSize];  // 存放队列元素
	int front;  // 队首
	int rear;  // 队尾 
}SqQueue;

队空：Q.front == Q.rear == 0

循环队列

存储方式

• 队头元素存储——data[(front+1) % maxSize]

• 队满——maxSize-1

• 队长——(rear- front) % maxSize

• 空队列——front == rear

• 满队列——(rear+1) % maxSize == font

• 队尾进1（入队）——rear = (rear+1) % maxSize

• 队头进1（出队）——front = (front+1) % maxSize

定义

typedef struct SqQueue{
    int front; //队头位置
    int rear; //队尾位置
    int maxSize; //队列容量
    ElemType *data; // 队列数组首地址
}SqQueue;

初始化

void InitQueue(SqQueue *Q, int mSize) //Q:队列首地址 mSize:最大容量
{
    Q->maxSize = mSize; // 最大容量赋值
    Q->data = (ElemType*)malloc(sizeof(ElemType)*mSize); // 为队列数组申请空间
    Q->front = Q->rear = 0; // 队头队尾归零
}

销毁（释放空间）

void DestroyQueue(SqQueue *Q)
{
    free(Q->data); //释放数组空间
    Q->maxSizw = -1; //最大容积归负
    Q->front = Q->rear = -1; //队头队尾归负
}

清除(不释放空间)

void Clear(Queue *Q)
{
    Q->front = Q->rear = 0; // 队头队尾归零
}

获取队头

bool GetFront(SqQueue *Q, ElemType *x)
{
    if(QueueEmpty(Q)) // 空队列
        return FALSE;
    *x = Q->data[(Q->front+1) % Q->maxSize]; // 取队头元素
    return TRUE;
}

入队

BOOL EnQueue(SqQueue *Q, ElemType x)
{
    if(QueueFull(Q)) // 溢出
        return FALSE;
    Q->rear = (Q->rear+1) % Q->maxSize; // 队尾进1
    Q->data[Q->rear] = x; // 队尾赋值
    return TRUE;
}

出队

BOOL DeQueue(SqQueue *Q, ElemType *x)
{
    if(IsEmpty(Q)) // 空队列
        return FALSE;
    *x = Q->data[(Q->front+1) % Q->maxSize]; // 取队头元素
    Q->front = (Q->front+1) % Q->maxSize; //队头进1
    return TRUE;
}

链式队列

定义

typedef struct{
	ElemType data; //数据域
    struct node *link; //指针域
}LinkNode;
typedef struct{
    LinkNode *front; //头指针
    LinkNode *rear; //尾指针
}LinkQueue;

• 队空：Q.front == Q.rear == NULL

初始化

void InitQueue(LinkQueue &Q){
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));  // 建立头结点
	Q.front->next = NULL;  //初始为空 
}

入队

void Enqueue(Queue *Q, ElemType x)
{
    Node *p = (Node*)malloc(sizeof(Node)); // 结点申请空间
    p->data = x; // 结点赋值
    p->link = NULL; // 结点指向空
    Q->rear->link = p; // 队列尾指向结点
    Q->rear = p; //结点作为队列尾
}

出队

void DeQueue(Queue *Q)
{
    if(Q->front == NULL) // 空队列
        return;
    Node *p = Q->front; //结点p移动到队头
    Q->front = p->link; //队头变为结点所指向的结点
    free(p); //释放结点
    
    if(Q->front == NULL) //若为空队，重置队尾
        Q->rear = NULL;
}

应用

表达式

• 中缀表达式
• 前缀表达式(波兰式)
• 后缀表达式(逆波兰式)

括号匹配

栈

递归

栈

函数

栈

主函数$\rightarrow$函数$\rightarrow$子函数

层次遍历

队列

计算机系统

缓冲区——队列

资源竞争——队列

总结比较

相同点

都是线性结构

不同点

	栈	队列
进出方式	先进后出 后进先出	先进先出 后进后出

考点

1. 输出序列

   • 由出栈序列判断容量：模拟进出栈
   • 以$x$元素开头的序列个数：将$x$元素之前的序列列出：$x,x-1,\cdots,1$，然后剩下的插空
   • 若入栈是$1,2,\cdots,n$；出栈是$p_1,p_2,\cdots,p_n$
     • 若$p_1=n$，则$p_i=n-i+1$
     • 若$p_1=n(1<i<n)$，则$p_i=n-i+1$，$p_i>p_{i+1}>\cdots>p_n$
     • 若$1、2、3$则无$3、1、2$
   • 共有$\dfrac{C^n_{2n}}{n+1}$种出栈顺序

2. 表达式转换

   每一个子表达式都用()括起来，然后移动符号到()外

3. 用栈实现表达式转换

   • 中缀转后缀
     • 从左开始扫描
     • 当前扫描的$\le$栈顶运算符，则栈顶运算符出栈
     • 当前扫描的$>$栈顶运算符，直接入栈
     • (直接入栈，当栈顶为(时，所有运算符均入栈
     • 扫描到)时，将其到(的所有运算符全部出栈
     • 扫描完，栈中全部出栈
   • 中缀转前缀
     • 从右开始扫描
     • 当前扫描的$<$栈顶运算符，则栈顶运算符出栈
     • 当前扫描的$\ge$栈顶运算符，直接入栈
     • )直接入栈，当栈顶为)时，所有运算符均入栈
     • 扫描到(时，将其到)的所有运算符全部出栈
     • 扫描完，栈中全部出栈
   • 后缀转前缀
     • 扫描到字母，符号从后到前

4. 配置

   • 正常配置(front指向队头前一个元素，rear指向队尾)

     队空：front == rear

     入队：rear = (rear + 1) % maxSize; Queue[rear] = x;

     出队： front = (front + 1) % maxSize; x = Queue[front];

     队满：front == (rear + 1) % maxSize;

     队中元素：(rear - front) % maxSize

   • front指向队头，rear指向队尾后一个位置

     队空：front == rear

     入队：Queue[rear] = x; rear = (rear + 1) % maxSize;

     (先移动元素，再移动指针)

     出队： x = Queue[front]; front = (front + 1) % maxSize;

     队满：front == (rear + 1) % maxSize;

     队中元素：(rear - front) % maxSize

   • 队空时rear在front后一

     队空：front == (rear + 1) % maxSize;

     入队：rear = (rear + 1) % maxSize; Queue[rear] = x;

     出队： front = (front + 1) % maxSize; x = Queue[front];

     队满：front == (rear + 2) % maxSize;

     队中元素：(rear - front + 1) % maxSize

5. 双端队列

6. 栈的扩展

   共享栈

   用栈模拟队列

   • 若$S_1$未满，则元素直接进入$S_1$
   • 若$S_1$满，$S_2$空，则$S_1$元素全部加入$S_1$
   • 若$S_2$不空，则$S_2$直接出栈
   • 若$S_2$空，则$S_1$元素全部出栈进入$S_2$，然后从$S_2$出栈
   • 队满：$S_1$满且$S_2$不空

7. 括号匹配

   /*左右匹配
   左右同为同种括号 
   */
   int isMatched(char left, char right){
   	if(left == '('  &&  right == ')')
   		return 1;
   	if(left == '['  &&  right == ']')
   		return 1;
   	if(left == '{'  &&  right == '}')
   		return 1;
   	else
   		return 0;
   } 
   /*
   括号匹配 
   */
   int isParenthesesBalances(char exp[]){
   	char s[maxSize];  // 栈 
   	int top = -1;  // 栈顶 
   	for(int i=0 ; exp[i] != '\0'; ++i){  // 字符串直到'\0'结束 
   		if(exp[i]=='('  ||  exp[i]=='['  ||exp[i]=='{')  // 左括号入栈 
   			s[++top] = exp[i];
   		if(exp[i]==')'  ||  exp[i]==']'  ||exp[i]=='}'){  // 右括号 
   			if(top == -1)  // 空栈直接错误 
   				return 0;
   			char left = s[top--];  // 提取栈顶 
   			if(isMatched(left, exp[i]) == 0)  // 若栈顶和右括号不匹配，错误 
   				return 0;
   		}
   	}
   	if(top > -1)  // 若还有剩余元素，错误 
   		return 0;
   	return 1;
   }

8. 计算问题