树

基本概念

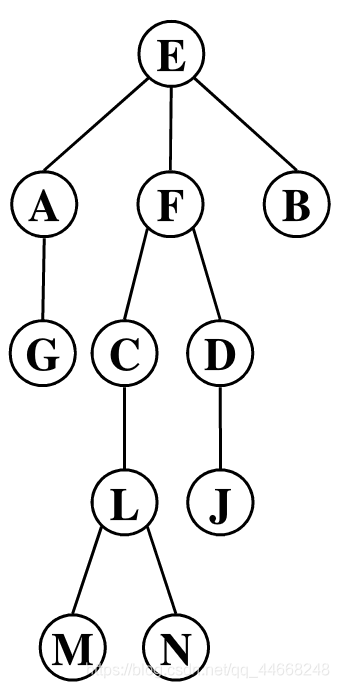
• 结点

• 边：根节点和子树跟之间

• 路径：从某个结点可达另一个结点(树有向：双亲$\rightarrow$孩子)

  树路径长度：路径总和

结点关系

• 双亲：该结点上连的点

• 孩子：该结点下连的点

• 兄弟：有共同双亲的结点

• 堂兄弟：双亲为兄弟的结点

• 后裔：子树的所有结点

• 祖先：向上到根结点所有的点

度

• 结点的度：结点的子树数

• 叶子：度为0的结点

• 分支节点：度不为0的结点

• 树的度：结点度最大值

树的高度

• 树的层次：树根为第一层
• 树的高度：最大层次

有序/无序

• 左右子树可/不可互换

树的性质

结点数$n$、度数$m$、高度$h$、层数$i$，总分支$k$

• $n=\sum m+1$
• $n(i)\le m^{i-1}$
• $h+m-1\le n\le\dfrac{m^h-1}{m-1}$
• $⌈\log_m(n(m-1)+1)⌉\le h\le n-m+1$
• $k=n_1+2n_2+\cdots+mn_m=n-1$

二叉树

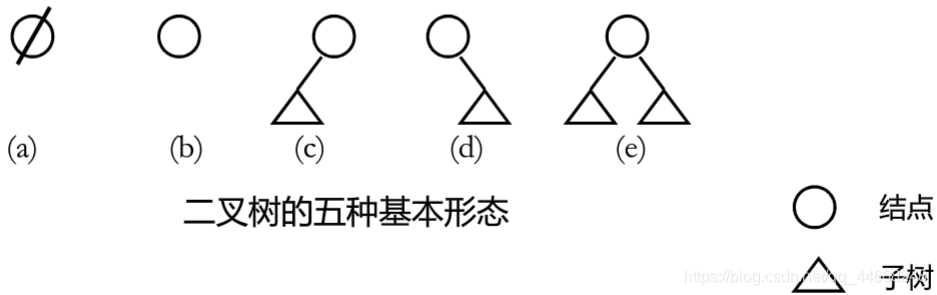
二叉树性质

1. $n(i)\le2^{i-1}$
2. $n\le 2^{h}-1$
3. $⌈\log_2(n+1)⌉{\leq}h{\leq}n$
4. $n_0=n_2+1$
5. 有$n+1$个空指针

特殊二叉树

满二叉树

高度为$h$，且$2^h-1$结点

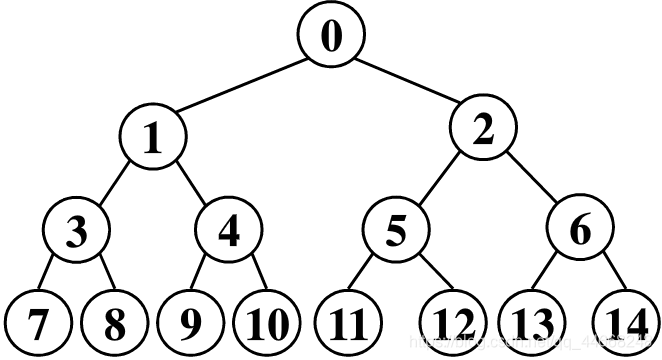
• 满二叉树一定是完全二叉树，也是扩充二叉树

完全二叉树

• 除最下面两层度小于$2$，其他层结点度均为$2$
• 最下一层叶结点均依次集中在靠左若干位置

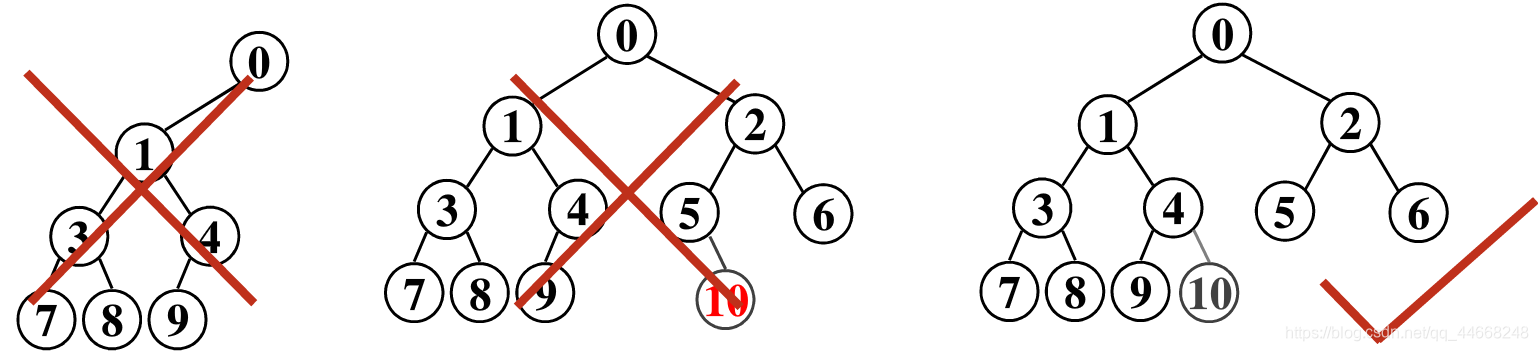
• 完全二叉树高度$h=[log_2(n+1)]$

• 所在层数：$i=⌊\log_2n⌋$

• 由上到下、由左到右、从$0$编号

  根——$i=0$

  双亲——$[\dfrac{i-1}{2}]$

  左孩子——$2i+1$

  右孩子——$2i+2$

• $n_0=n(i>⌊\dfrac2n⌋)$

• $n_1$只能取$0$或$1$

  若$n_1=1$，则该结点有左子无右子

扩充二叉树（2-树）

• 除叶子结点，必须有两个孩子
• 仅有度$2$和$0$的结点，不存在度为$1$的结点

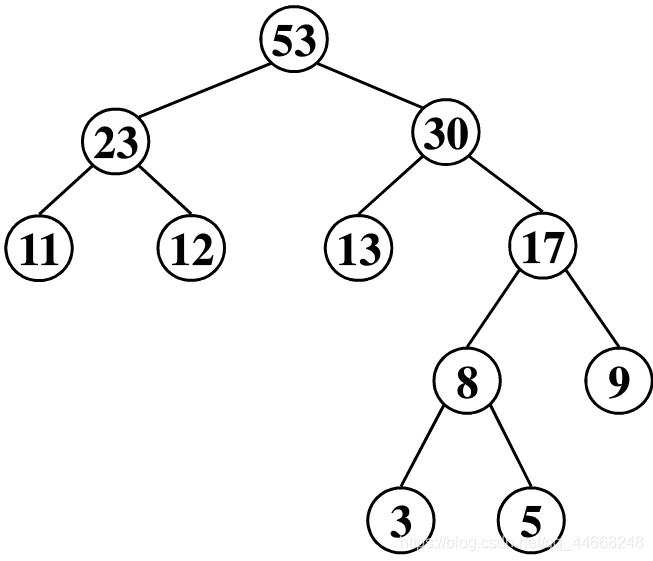
二叉排序树

左结点 $<$ 根结点 $<$ 右结点

平衡二叉树

$\left|h_{左}-h_{右}\right|\le1$

代码

链接表示

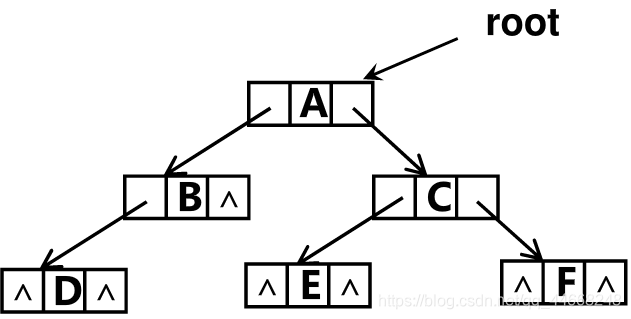
typedef struct BiTNode{
    ElemType data; // 数据域
    struct BiTNode* lChild; // 左孩子指针
    struct BiTNode* rChild; // 右孩子指针
}BiTNode, *BiTree;

• 在$n$个结点的二叉链表中，有$n+1$个空链域

创建空二叉树

void Create(BinaryTree *bt)
{
    bt->root = NULL;
}

创建新结点

BTNode* NewNode(ElemType x, BTNode *ln, BTNode *rn)
{
    BTNode *p = (BTNode*)malloc(sizeof(BTNode)); // 申请空间
    p->element = x; // 结点内容赋值
    p->lChild = ln; // 左子树赋值
    p->rChild = rn; // 右子树赋值
    return p;
}

返回根结点

BOOL Root(BinaryTree *bt, ElemType *x)
{
    if(!bt->boot) // 空树
        return FALSE;
    else
    {
        *x = bt->root->element; // 赋值
        return TRUE;
    }
}

构造二叉树

void MakeTree(BinaryTree *bt, ElemType e, BinaryTree *left, BinaryTree *right) // bt:根地址 e:根值 left:左子树 right:右子树
{
    if(bt->root || left==right)
        return;
    bt->root = NewNode(e,left->root,right->root);
    left->root = right->root = NULL;
}

遍历

先序遍历+后序遍历不可确定二叉树：$\left. \begin{array}{r} \text{前序}XY\\ \text{后序}YX\\ \end{array} \right\} \Rightarrow X$为$Y$祖先

先序遍历

步骤：

1. 先访问根结点

2. 先序遍历左子树

3. 先序遍历右子树

特性

• 最先访问的是根结点
• $n$个元素先序遍历二叉树共$\dfrac{\text C^n_{2n}}{n+1}$

递归代码

void PreOrder(BiTree T) // 先序遍历递归函数
{
    if(!T) // 树空了直接返回
        return;
    visit(T); //访问根结点
    PreOrder(T->lChild); // 先序遍历左子树
    PreOrder(T->rChild); // 先序遍历右子树
}

时间复杂度：$O(n)$

非递归代码

void PreOrder(BiTree T){  // 中序遍历 
	InitStack(S);  // 初始化栈 
	BiTree p = T;  // 结点指向根结点 
	while(p || !IsEmpty(S)){  // 当p存在且栈不空 
		if(p){  // 若p存在，入栈且前往左孩子 
			visit(p);
			push(S, p);
			p = p->lchild;
		}
		else{  // 若p不存在则出栈访问且前往右孩子 
			Pop(S, p);
			p = p->rchild;
		}
	}
}

中序遍历

步骤

1. 中序遍历左子树
2. 访问根结点
3. 中序遍历右子树

特性

• 左子树中所有结点先于根结点
• 右子树中所有结点后于根结点

递归代码

void InOrder(BiTree T) // 中序遍历递归函数
{
    if(!t) // 树空了直接返回
        return;
    InOrder(T->lChild); // 中序遍历左子树
    visit(T); //访问根结点
    InOrder(T->rChild); // 中序遍历右子树
}

时间复杂度：$O(n)$

非递归代码

void InOrder(BiTree T){  // 中序遍历 
	InitStack(S);  // 初始化栈 
	BiTree p = T;  // 结点指向根结点 
	while(p || !IsEmpty(S)){  // 当p存在且栈不空 
		if(p){  // 若p存在，入栈且前往左孩子 
			push(S, p);
			p = p->lchild;
		}
		else{  // 若p不存在则出栈访问且前往右孩子 
			Pop(S, p);
			visit(p);
			p = p->rchild;
		}
	}
}

后序遍历

步骤

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根结点

特性

• 最后访问根结点

代码

void PostOrder(BiTree T) // 后序遍历递归函数
{
    if(!t) // 树空了直接返回
        return;
    PostOrder(T->lChild); // 后序遍历左子树
    PostOrder(T->rChild); // 后序遍历右子树
    visit(T); //访问根结点
}

时间复杂度：$O(n)$

非递归算法

/**/
void postOrder(BTNode T){
	if(!T)
        return;
    InitStack(S);  // 辅助遍历栈 
	BiNode p = T;// p指向根结点
    r = NULL;  // 记录最近访问的结点
    while(p || !IsEmpty(s)){  // 当p存在且栈不空
        if(p){
        	push(S, p);  // 根结点结点入栈
        	p = p->lChild; // 访问左孩子
        }
    }else{
        getTop(S, p);  // 读取栈顶元素（不出栈）
        if(p->rChild && p->rChild != r)  // 右子树存在且从未被访问
            p = p->rChild;  // 转向右子树
        else{
            pop(S, p);  // 出栈
            visit(p->data);  // 访问该结点
            r = p;  
            p = NULL;  // 重置
        }
    }
} 

层次遍历

步骤

• 若二叉树为空，直接退出

  否则，初始化队列

  再将根结点进队

• 若队列不为空

• 1. 获取队头结点$p$，并将队头结点出队
  2. 访问结点$p$中的数据
  3. $p$的左孩子进队
  4. $p$的右孩子进队

代码

void LevelOrderTree(BiTree *T)
{
    Queue Q; // 存储BTNode结点类型指针的队列
    BTNode p = T;
    if(!T) // 二叉树为空
        return;
    Create(&Q, T); // 初始化队列
    EnQueue(&Q, T); // 根结点进队
    while(!IsEmpty(&Q))
    {
        DeQueue(Q,p); // 获取队头结点
        visit(p); // 访问结点p
        if(p->lChild) 
            EnQueue(Q,p->lChild); //若左孩子存在，则进队
        if(p->rChild) 
            EnQueue(Q,p->rChild); //若右孩子存在，则进队
    }
    Destroy(&Q); // 销毁队列
}

线索二叉树

目的：加快二叉树遍历（加快查找结点前驱后驱）

• 先序线索二叉树：查找先序后继，先序前驱
• 后序线索二叉树：查找后序前驱，后序后继

结构：物理结构（链表）

线索个数：$n+1$

空链域：$2$

存储结构

lChild

ltag

data

rtag

rchild

• $\text{ltag}=\left\{ \begin{array}{l} 0\ \ \text{lchild指向左孩子}\\ 1\ \ \text{lchild指向前驱}\\ \end{array} \right. $
• $\text{rtag}=\left\{ \begin{array}{l} 0\ \ \text{rchild指向右孩子}\\ 1\ \ \text{rchild指向后驱}\\ \end{array} \right. $

typedef struct ThreadNode{
	ElemType data; //数据域
    struct ThreadNode* lchild; // 左孩子 
    struct ThreadNode* rchild; // 右孩子  
    int ltag;  // 左指标
	int rtag;  // 右指标 
}ThreadNode, *ThreadTree;

前序遍历线索树

void preThread(TBNode *p, ThreadTree &pre){
	if(p){
		if(!p->lchild){  // 左子树为空，建立前驱结点 
			p->lchild = pre;
			p->ltag = 1;
		}
		if(pre && !pre->rchild){  // 建立前驱结点后继搜索 
			pre->rchild = p;
			pre->rtag = 1;
		}
		pre = p;  // 标记当前结点为刚刚访问的结点 
		preThread(p->lchild, pre);
		preThread(p->rchild, pre);
	}
}

中序遍历线索树

void InThread(ThreadTree &p, ThreadTree &pre){  // P：正在访问的结点；pre：刚刚访问的结点
	if(p){
		InThread(p->lchild, pre);  // 递归线索化左子树 
		if(!p->lchild){  // 左子树为空，建立前驱结点 
			p->lchild = pre;
			p->ltag = 1;
		}
		if(pre && !pre->rchild){  // 建立前驱结点后继搜索 
			pre->rchild = p;
			pre->rtag = 1;
		}
		pre = p;  // 标记当前结点为刚刚访问的结点 
		InThread(p->rchild, pre);  // 线索化右子树 
	}
}

void CreateInThread(ThreadTree T){
	ThreadTree pre = NULL;  // 刚开始无刚访问的结点 
	if(T){
		InThread(T, pre);  // 线索化非空二叉树 
		pre->rchild = NULL;  // 处理最后一个结点 
		pre->rtag = 1;
	}
}

后序遍历线索树

void postThread(ThreadTree &p, ThreadTree &pre){
	if(p){
		postThread(p->lchild, pre);  // 递归线索化左子树 
		postThread(p->rchild, pre); 
		if(!p->lchild){  // 左子树为空，建立前驱结点 
			p->lchild = pre;
			p->ltag = 1;
		}
		if(pre && !pre->rchild){  // 建立前驱结点后继搜索 
			pre->rchild = p;
			pre->rtag = 1;
		}
		pre = p;  // 标记当前结点为刚刚访问的结点 	
	}
}

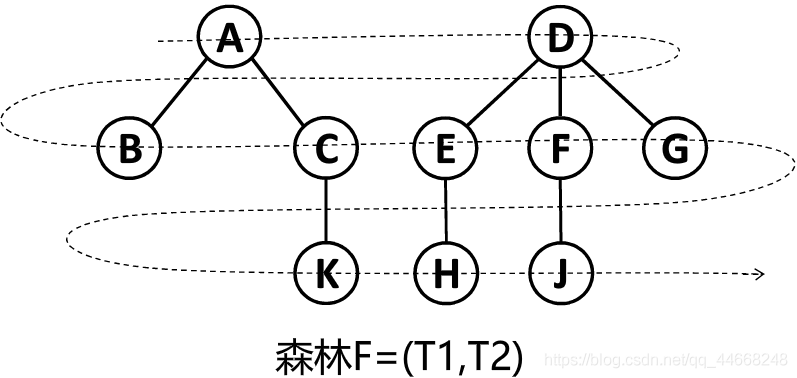
森林

森林遍历

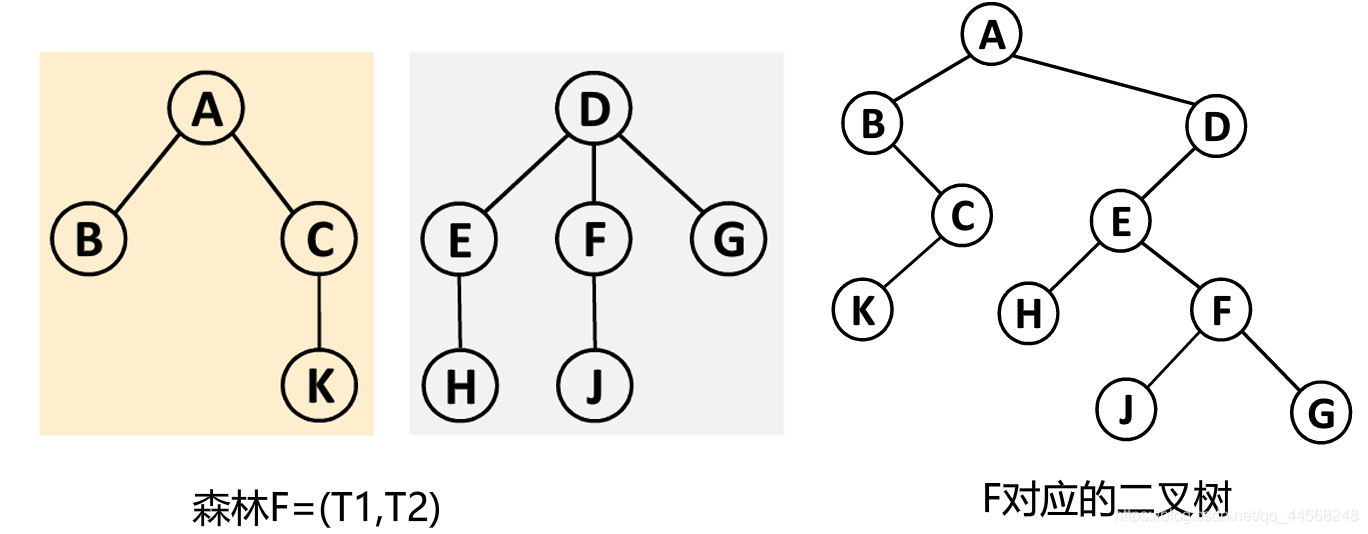
先序遍历

若森林为空，则结束

1. 访问第一棵树根

2. 第一棵树的根结点子树构成的森林

3. 先序遍历其他树

• 先序遍历等于每棵树先序遍历简单拼接

中序遍历

若森林为空，则遍历结束;否则

1. 中序遍历第一棵树的根结点的子树构成的森林
2. 访问第一棵树的根
3. 中序遍历其他树

• 中序遍历等于每棵树中序遍历简单拼接

后序遍历

若森林为空，则遍历结束;否则

1. 后序遍历第一棵树的根结点的子树构成的森林
2. 后序遍历其他树
3. 访问第一棵树的根

• 后序遍历不等于每棵树中序遍历简单拼接
• 不常用

层次遍历

1. 访问第一层所有结点
2. 访问第二层所有结点
3. $……$

堆

存储方式

• 最后一个叶子结点双亲位置——$[\dfrac{n-2}{2}]$
• 根结点位置——$0$

最小堆

每个结点数据小于等于孩子结点

最大堆

每个结点数据大于等于孩子结点

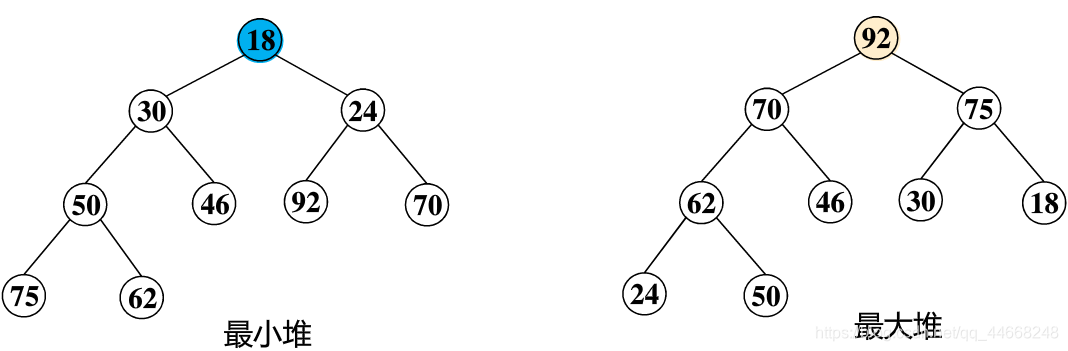
堆的判断

最小堆

$k_i{\leq}k_{2i+1}$和$k_i{\leq}k_{2i+2}$

最大堆

$k_i{\geq}k_{2i+1}$和$k_i{\geq}k_{2i+2}$

建堆运算

从最后叶子的双亲$k_{[\frac{n-2}{2}]}$反方向直到根结点$k_0$，依次对每个结点$k_i$

1. 若该结点小于（大于）或等于其孩子，则结束
2. 将该结点与与最小（大）孩子交换

代码

向下调整算法

void AdjustDown(ElemType heap[], int current, int border) // heap:存放序列数组 current:当前待调整序列中的位置 border:待调整序列的边界
{
    int p = current;
    int minChild;
    ElemType temp;
    while(2*p+1 <= border) // 若p不是叶结点
    {
        if((2*p+2 <= border) && (heap[2*p+1] > heap[2*p+2])) // 右孩子存在 右孩子较小
            minChild = 2*p+2;
        else // 右孩子不存在 或 右孩子较大
            minChild = 2*p+1; 
        
        if(heap[p] <= heap[minChild]) // 若当前结点不大于其最小的孩子，结束
            break;
        else // 否则将p和其最小孩子交换
        {
            temp = heap[p] ; heap[p] = heap[minChild] ; heap[minChild] = temp;
            p = minChild; // 当前下移元素的位置
        }
    }
}

建堆算法

void CreateHeap(ElemType heap[], int n)
{
    int i;
    for(i=(n-2)/2 ; i>-1 ;i--) // 从最后一个叶结点的双亲反向到根结点
        AdjustDown(heap,i,n-1); // 依次执行向下调整
}

性能

建堆：$O(n)$

插入：$O(\log_2n)$

删除：$O(\log_2n)$

优先权队列

• 元素加入次序无关紧要
• 出队只取最高优先级的元素

实现方案

进队

• 将新元素放堆尾，并按照最小堆（或最大堆）进行调整$O(log_2n)$

出队

• 直接取出堆顶元素$O(1)$
• 按照最小堆（或最大堆）进行适当调整$O(log_2n)$

存储方式

代码

typedef struct priorityQueue
{
    ElemType *element; // 存储元素数据
    int n; // 元素个数
    int maxSize; // 优先队列容量
}PriorityQueue;

向上调整AdjustUp

代码

void AdjustUp(ElemType heap[], int current) // heap:最小堆数组 current:新元素位置
{
    int p =current; // 让p指向新元素位置
    ElemType temp;
    while(p>0) // p指向根结点循环结束
    {
        if(heap[p] < heap[(p-1)/2]) // p指向元素小于其父节点，则与父节点交换
        {
            temp=heap[p] ; heap[p]=heap[(p-1)/2] ; heap[(p-1)/2]=temp;
            p = (p-1)/2; // p向上移动至父节点位置
        }
        else // 若p指向结点不小于其父节点，则调整完毕
            break;
    }
}

时间复杂度

$O(log_2n)$

优先权队列实现

创建空优先权队列

void CreatePQ(PriorityQueue *PQ, int mSize)
{
    PQ->maxSize = mSize; // PQ最大容量赋值
    PQ->n = 0; // PQ元素个数为0
    PQ->element = (ElemType*)malloc(mSize*sizeof(ElemType)); // 申请空间
}

销毁队列，释放空间

void Destroy(PriorityQueue *PQ)
{
    free(PQ->element); // 释放数组空间
    PQ->n = 0; // PQ元素个数为0
    PQ->maxSize = 0; // PQ容量清零
}

增加新元素

void Append(PriorityQueue *PQ, ElemType x)
{
    if(IsFull(PQ)) //满队
        return;
    PQ->element[PQ->n] = x; // 优先权队列最后一个元素后面插入一个元素
    PQ->n++; // 元素数量+1
    AdjustUp(PQ->element, PQ->n-1); // 新增元素向上调整
}

时间复杂度$O(log_2n)$

取出优先权最高队列

void Serve(PriorityQueue *PQ, ElemType *x)
{
    if(IsEmpty(PQ)) // 空队
        return;
    *x = PQ->element[0]; // 栈顶元素赋值
    PQ->n--; // 元素个数-1
    PQ->element[0] = PQ->element[PQ->n]; // 用堆尾替代堆顶元素
    AdjustDown(PQ->element, 0, PQ->n-1); // 向上调整
}

时间复杂度$O(log_2n)$

树的应用

二叉搜索树BST

存储方式

• 左子树小于根结点
• 右子树大于根结点
• 若以中序遍历二叉搜索树，将得到递增有序序列

性质

• 高度(搜索次数)：$\lceil\log_2(n+1)\rceil\le h\le n$

代码

搜索

查找关键字$x$

1. 二叉树为空，搜索失败
2. 将$x$与根结点比较
   • $k$小于该结点，搜索左子树
   • $k$大于该结点，搜索右子树
   • $k$等于该结点，搜索成功

递归算法

BSTNode *Find(BSTNode *T,KeyType key)
{
    if(!T)
        return NULL; // 搜索失败
    if(T->data == key)
        return T; // 搜索成功
    if(T->data < key)
        return Find(T->lChild, key);
    return Find(T->rChild, key);
}

迭代算法

BOOL BtSearch(Btree Bt,KeyType k,T *x)
{
    BTNode *p = Bt.Root; // 从根结点出发
    while(p)
    {
        if(k < p->element.key) // 从左分支继续向下搜索
            p = p->lChild;
        else if(k > p->element.key) // 从右分支继续向下搜索
            p = p->rChild;
        else
        {
            *x = p->element; // 搜索成功
            return TRUE;
        }
    }
    return FALSE;
}

插入

• 向下搜索$x$
• 搜索失败处插入$x$

递归

int BSTInsert(BiTree &T, KeyType key){
    if(T == NULL){  // 树为空，创造空间插入结点
        T = (BiTree)malloc(sizeof(BSTNode));
        T->key = k;
        T->lchild = T->rchild = NULL;
        return 1; // 插入成功
    }else if(k == T.key)  // 存在了相同关键字，插入失败
        return 0;
     else if(k < T.key)  // 插入到左子树
         return BSTInsert(T->lchild, k);
     else  // 插入右子树
         return BSTInsert(T->rchild, k);
}

非递归

BOOL Insert(Btree *bt, T x)
{
    BTNode *p = bt->root, *q, *r; // p:从根节点向下搜索 q:记录搜索失败上一层结点
    KeyType k = x.key;
    while(p)
    {
        q = p;
        if(k < p->element.key)
            p = p->lChild;
        else if(k > p->element.key)
            p = p->rChild;
        else
            return FALSE;
    }
}

删除

删除叶子结点

直接删

1. 将待删除结点双亲结点指向NULL
2. 释放待删除结点

删除有一个孩子结点

爷带孙

1. 待删除结点的双亲结点指向待删除结点的孩子
2. 释放待删除结点

删除有两个孩子结点

1. 从后代选择一个覆盖待删除结点
   • 保持二叉搜索树有序性==左孩子$\leq$代替这$\leq$右孩子==
   • 容易删除==只有一个孩子或没有孩子==
2. 删除重复的代替者

代替者选择方法

• 选择其中序遍历的直接前驱
  • 为左子树最大值
  • 一定没有右孩子
• 选择其中序遍历的直接后驱
  • 为右子树最小值
  • 一定没有左孩子

二叉平衡树

定义

• 二叉搜索树
• 左右子树高度差$h’\leq{1}$
• 左右子树都是二叉平衡树

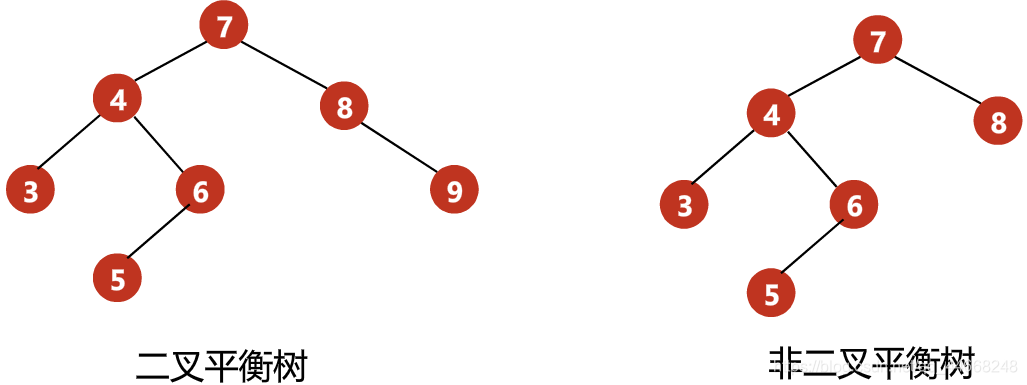
• 平衡因子——左子树与右子树高度差$h_{left}-h_{right}$

性质

• 最少结点：$n_h=\left\{ \begin{array}{l} 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ h=0\\ 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ h=1\\ 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ h=2\\ 1+n_{h-1}+n_{h-2}\ \ \ \ h\ne0,1,2 \\ \end{array} \right. $

二叉平衡树插入

• 先按照普通二叉搜索树插入

• 若不平衡，则进行调整

  • 先找到平衡因子超过$1$的根结点$s$

    1. $LL/RR$类型——单旋转

       新结点插入$s$的左/右结点

       

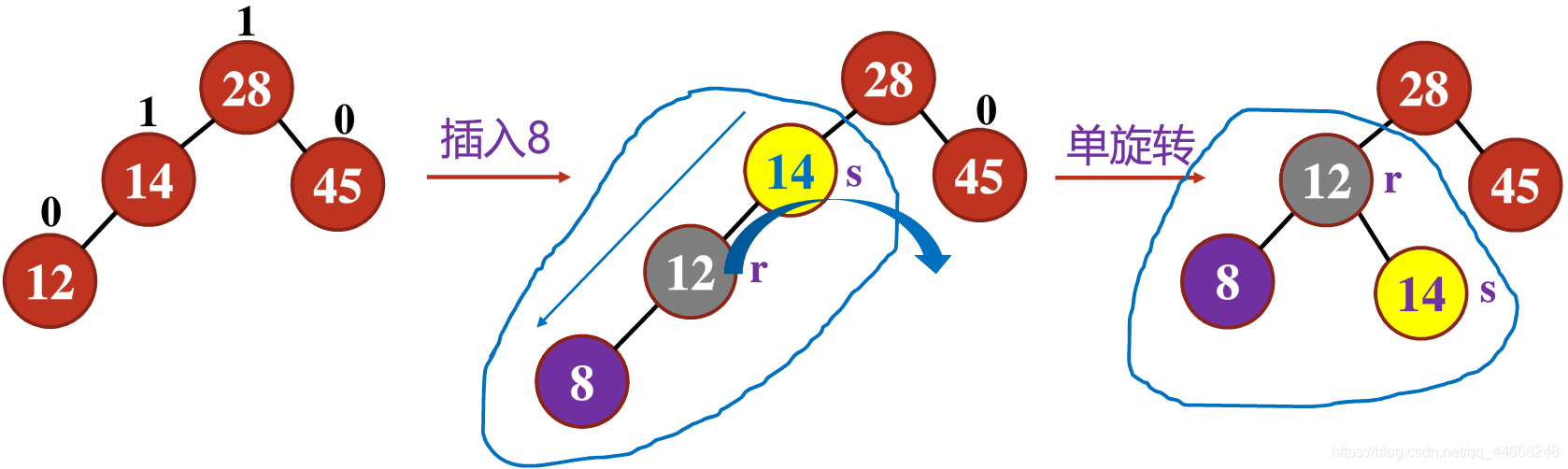
    2. $LR/RL$类型——双旋转

       

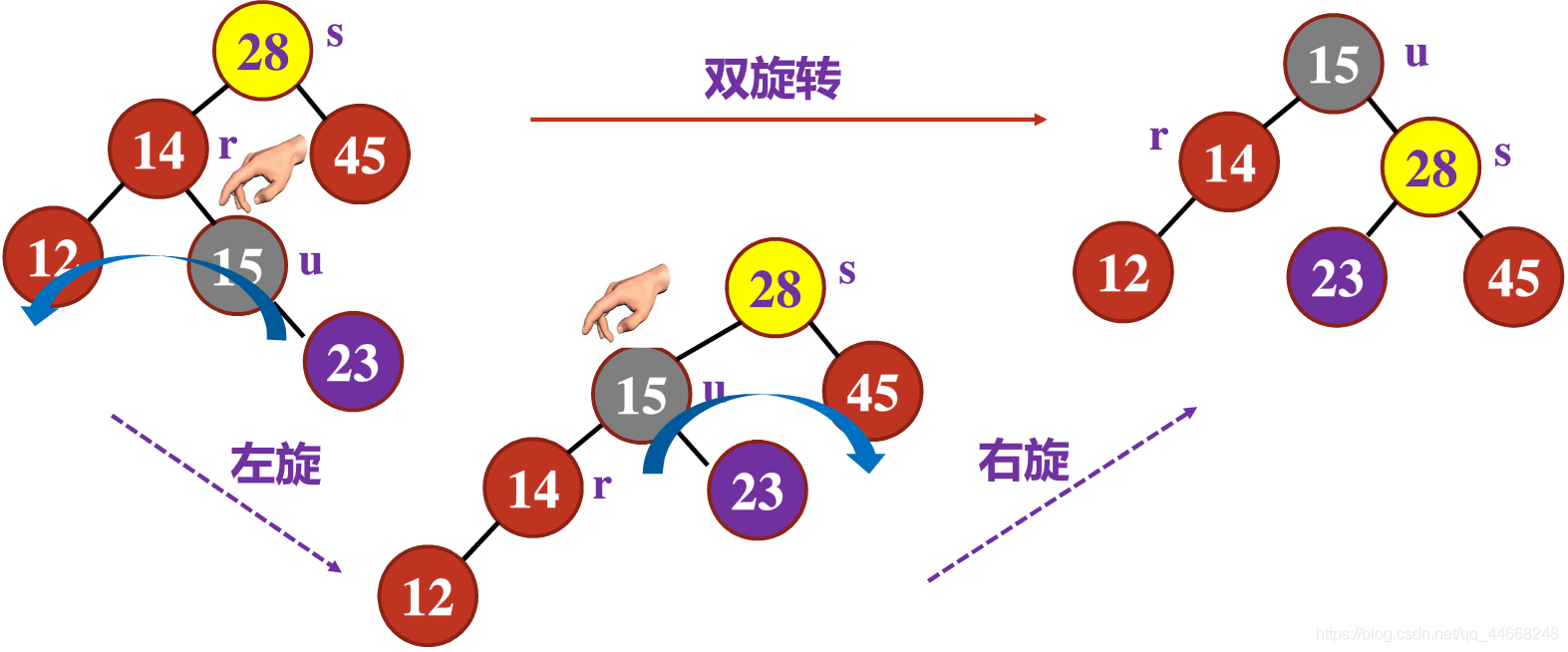
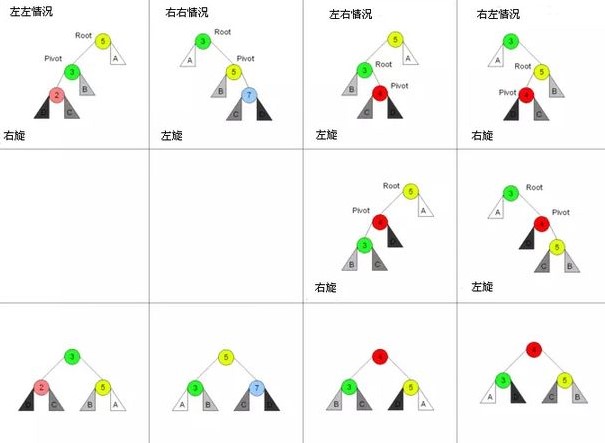
哈夫曼树

性质

• 哈夫曼树只有度为$0$和$2$的结点
• $n$个叶子结点共$n-1$非叶子结点
• 叶子结点：$(n+1)/2$

树路径长度

$E=I+2n$

• $I$——内路径长度

  根到分支结点路径和

• $E$——外路径长度

  根到叶子的路径长度

加权路径长度

$WPL={\sum}_{k=1}^mw_kl_k$

• $m$——叶结点数量
• $w_k$第$k$个叶结点权值
• $l_k$该叶结点路径长度
• $WPL$——文本最终转换成编码的总编码长度

哈夫曼树

• 哈夫曼树是最小加权路径长度的扩充二叉树
• 分支节点权值$=$左孩子权值$+$右孩子权值
• 对于$m$叉哈夫曼树，若$(n-1)%(m-1)=u\ne 0$，则需补充$m-u-1$个$0$叶结点

实现方法

1. 选取最小的两个值
2. 求和形成新的值，并与剩下的最小的求和

代码

BinaryTree CreateHFMTree(int w[], int m)
{
    BinaryTree x,y,z; // 二叉树变量
    Create(PQ,m); // 初始化优先权队列PQ, 优先权存在根结点数据域
    for(int i=0 ; i<m ; i++)
    {
        MakeTree(x,w[i],NULL,NULL); // 创建仅包含根结点二叉树，权值w[i]存入根结点
        Append(PQ,x); // 将二叉树x插入优先权队列
    }
    while(PQ.n > 1)
    {
        Serve(PQ,x); // 从PQ中取出根结点权值最小的二叉树，存入x
        Serve(PQ,y); // 从PQ中取出根结点权值最小的二叉树，存入y
    }
    /*合并二叉树x,y*/
    if(x.root.element < y.root.element) // 左子树结点权值小于右子树
        MakeTree(z, x.root.element+x.root.element, x, y);
    else
        MakeTree(z, x.root.element+x.root.element, y, x);
    Append(PQ, z); // 新合成新二叉树z插入优先权队列
Serve(PQ, x); // 获取优先权队列唯一二叉树，存入x，该二叉树即哈夫曼树
return x;
}

哈夫曼编码

• 左0右1
• 前缀编码：集合中元素不得为另一元素的前缀
• 编码对应哈夫曼树元素无子树

考点

1. 线索二叉树

2. 哈夫曼树

3. 二叉树的确定

4. 二叉树的估计

   将对应序列用T、L、R表示

   • 前序遍历与后序遍历相同：TLR、LRT
   • 前序遍历与中序遍历相同：TLR、LTR
   • 中序遍历与后序遍历相同：LTR、LRT
   • 前序遍历与后序遍历相反：TLR、LRT
   • 前序遍历与中序遍历相反：TLR、LTR
   • 中序遍历与后序遍历相反：LTR、LRT

5. 二叉树表达式