集合和搜索

搜索

顺序搜索

无序表顺序搜索

步骤

1. 从头开始检查，将指定元素$x$与关键字比较
2. • 若相等搜索成功
   • 若搜索完整个表，不存在，则搜索失败

代码

int SeqSearch(ListSet L, ElemType x)
{
    int i;
    for(i=0 ; i < L.n ; i++)
        if(L.element[i] == x)
            return i; // 搜索成功
    return -1; // 搜索失败
}

索引效率

$\text{ASL}_{成功}=\dfrac{n+1}{2}$

$\text{ASL}_{失败}=n+1$

有序表顺序搜索

• 关键字值满足$key_i{\leq}key_{i+1}$
• $key_i$表示$a_i$的关键字

步骤

1. 从头开始检查，将指定元素$x$与关键字比较
2. • 若相等搜索成功
   • 若某个元素关键字大于指定元素$x$，则搜索失败

代码

无哨兵

int SeqSearch(ListSet L, ElemType x)
{
    int i;
    for(i=0 ; i < L.n ; i++)
    {
        if(L.element[i] == x)
            return i; // 搜索成功
        else if(L.element[i] > x)
            return -1; // 搜索失败
    }
    return -1; // 搜索失败
}

有哨兵

int SeqSearch(ListSet L, ElemType x)
{
    int i;
    L.element[L.n] = MaxNum; // MaxNum正无穷
    for(i=0 ; L.element[i] < x ; i++)
        if(L.element[i] == x)
            return i; // 搜索成功
    return -1; // 搜索失败
}

索引效率

$\text{ASL}_{成功}=\dfrac{n+1}{2}$

$\text{ASL}_{失败}=\dfrac{n}{2}+{\dfrac{n}{n+1}}$

二分搜索

步骤

有序表$(a_0,a_1,a_2,……,a_{n-1})$

• 有序表长$L\leq{0}$，搜索失败
• 有序表长$L{\geq}0$，取某个元素$a_m$与$x$比较
  • $a_m.key = x.key$，搜索成功
  • $a_m.key>x.key$，二分搜索$(a_0,a_1,a_2,…,a_{m-1})$
  • $a_m.key<x.key$，二分搜索$(a_{m+1},a_{m+2},…,a_{n-1})$

代码

int BinarySearch(SeqList L, ElemType key){
	int low = 0;  // 起始点
	int high = L.length-1;  // 终点
	int mid;  // 中点
	while(low <= high){
		mid = (low + high) / 2;  // 取中值
		if(L.data[mid] == key)  // 查找成功
			return mid;
		else if(L.data[mid] > key)  // 在右侧
			high = mid - 1;
		else  // 在左侧
			low = mid + 1; 
	} 
	return false;  // 查找失败 
}

索引效率

$\text{ASL}=\log_2(n+1)-1$

$S_{success}=\dfrac{2^n(n-1)+k(n+1)+1}{N}$($N=2^n-1+k$ )

$S_{fail}=\dfrac{n2^n+(n+2)k}{2^n+k}$

步骤

有序表$(a_0,a_1,a_2,……,a_{n-1})$

• 有序表长$L\leq{0}$，搜索失败

• 有序表长$L{\geq}0$，取某个元素$a_{m}$与$x$比较

  $m=\dfrac{low+high}{2}$,$low=0,high=n-1$

  • $a_m.key = x.key$，搜索成功
  • $a_m.key>x.key$，二分搜索$(a_0,a_1,a_2,…,a_{m-1})$
  • $a_m.key<x.key$，二分搜索$(a_{m+1},a_{m+2},…,a_{n-1})$

代码

递归算法

int BinSearch(ListSet L, ElemType x, int low, int high)
{
    if(low <= high)
    {
        int m = (low+high) / 2; // 对半分割
        if(x < L.element[m])
            return BinSearch(L,x,low,m-1);
        else if(x > L.element[m])
            return BinSearch(L,x,m+1,high);
        else
            return m; // 搜索成功
    }
    return -1; // 搜索成功
}

迭代算法

int BinSearch(ListSet L, ElemType x)
{
    int m,kow = 0;high = L.n-1;
    while(low <= high)
    {
        m = (low+high)/2; // 对半分割
        if(x < L.element[m])
            high = m-1;
        else if(x > L.element[m])
            low = m+1;
        else
            return m;
    }
    return -1;
}

分块查找

$\text{ASL}=L_l+L_s$

存储结构：块间有序、块内无序

搜索步骤：先根据索引表确定所在分块，再在块内搜索

最优分块：$\sqrt n$，均采用折半查找效率最高

搜索树

m叉搜索树

存储方式

• 空树——失败结点

• 失败结点不是叶子节点

• 根结点最多$m$棵子树

  
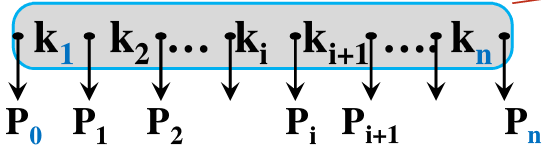
  • $k_i$是元素关键字
  • $P_i$是指向子树的指针
  • $n$为该结点元素个数，$1{\leq}n{\leq}m$

• 子树$P_i$所有关键字大于$K_i$，小于$K_{i+1}$

• 子树$P_0$所有关键字值小于$K_1$

  子树$P_n$上所有关键字大于$K_n$

• 子树$P_i(0{\leq}i{\leq}n)$也是$m$叉二叉树

• 结点最多存放m-1个元素和m个指针

• 结点里元素个数比包含指针少$1$

性质

1. 高度为$h$的$m$二叉树最多$m^h-1$个元素

   高度为$h$的$m$二叉树最多$\dfrac{m^h-1}{m-1}$个结点

2. 含有$N$个元素的$m$叉搜索树高度$h$满足$h{\leq}log_m(N+1)$

B树

性质

• 一个结点最多$m$个孩子，$m-1$个关键字
• 除根结点与失败结点每个结点至少$[\dfrac{m}{2} ]$个孩子，$[\dfrac{m}{2} ]-1$个关键字
• 根结点最少2个孩子
• 失败结点均在同一层，失败结点的双亲是叶子结点
• 失败结点：$n+1$;
• B树高度(磁盘存取次数)：$\log_m(n+1)\le h{\leq}\log_{\left\lceil\dfrac{m}{2}\right\rceil}{\dfrac{n+1}{2}}+1$
• 关键字：$k\ge (n-1)\left(\left \lceil \dfrac m2 \right \rceil-1\right)+1$

搜索

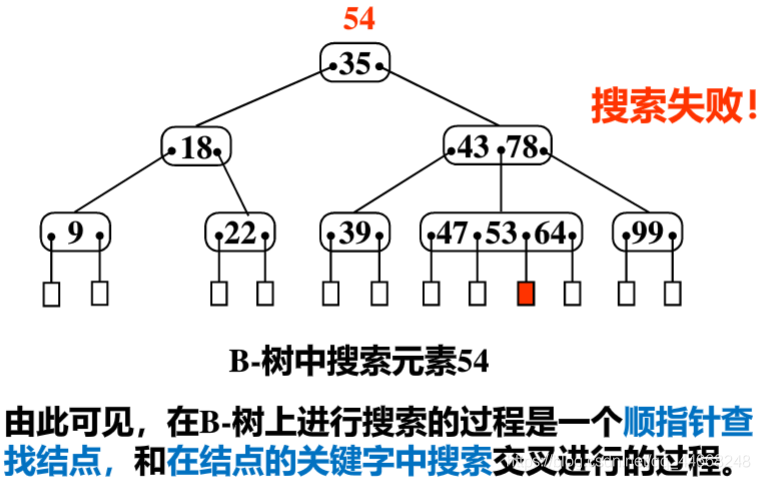
1. $B-$树中找结点，执行访问磁盘次数最多$log_{\frac{m}{2}}{\dfrac{N+1}{2}}$
2. 结点中找关键字

插入

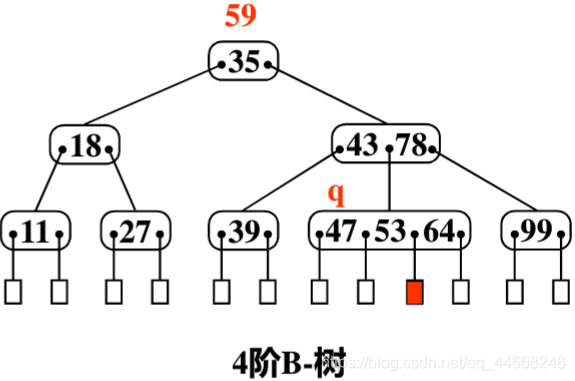
步骤

1. 搜索待插入元素

   若已存在，则插入失败

2. 插入停留的失败结点的叶子结点中

3. 将结点分为{$1$~${\dfrac{m}{2}-1}$}、{$\dfrac{m}{2}$}、{${\dfrac{m}{2}}$~$m$}

4. 将{$\dfrac{m}{2}$}和其指针插入其双亲结点

   • 根结点会向上形成一个新的根结点

删除

步骤

1. 叶子结点直接删除

2. 否则以其右子树最小元素替换

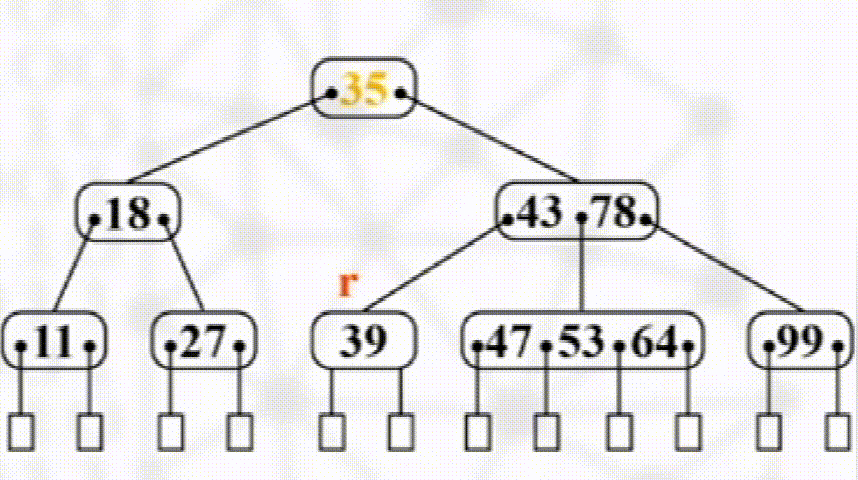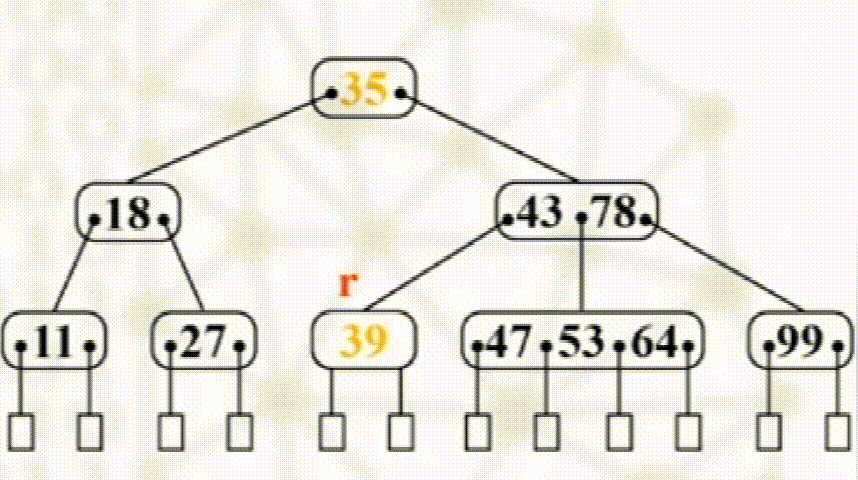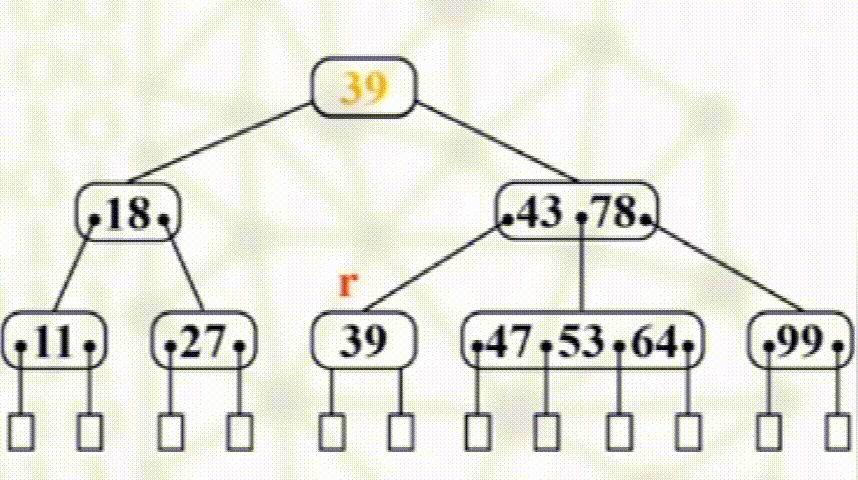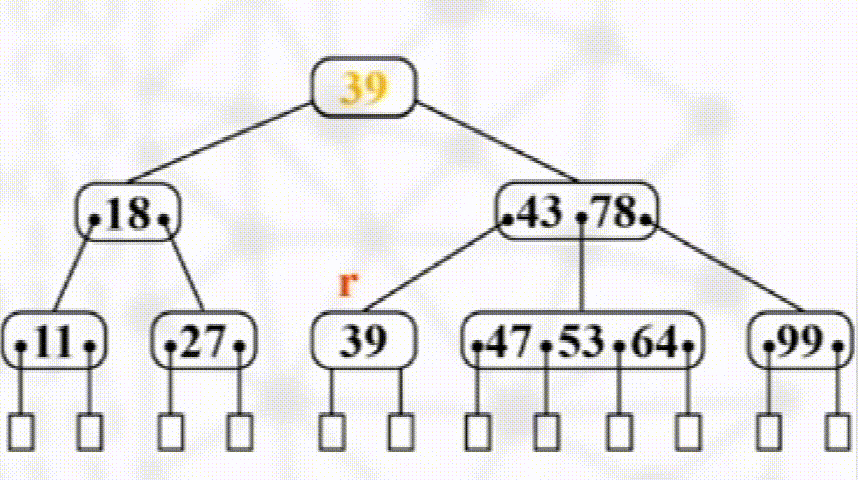
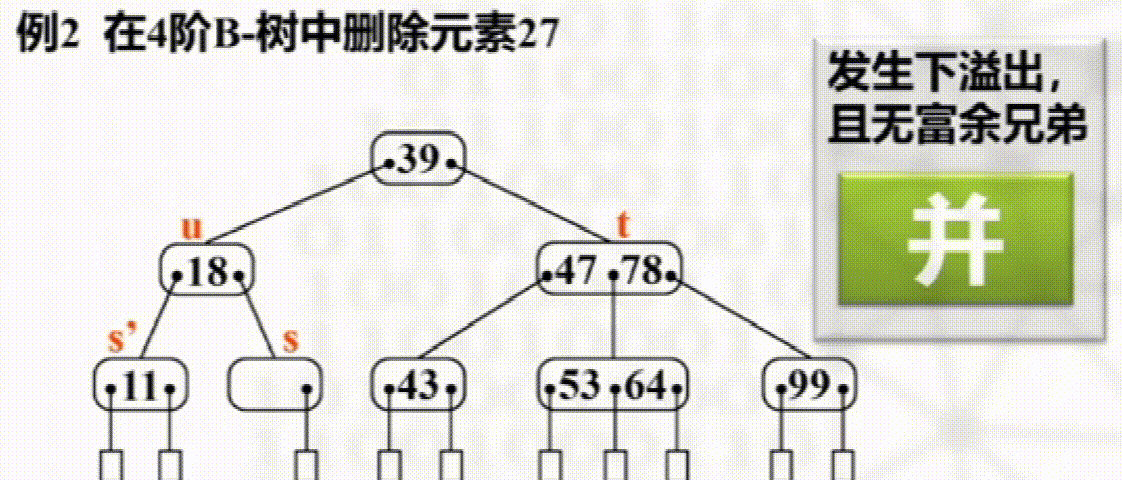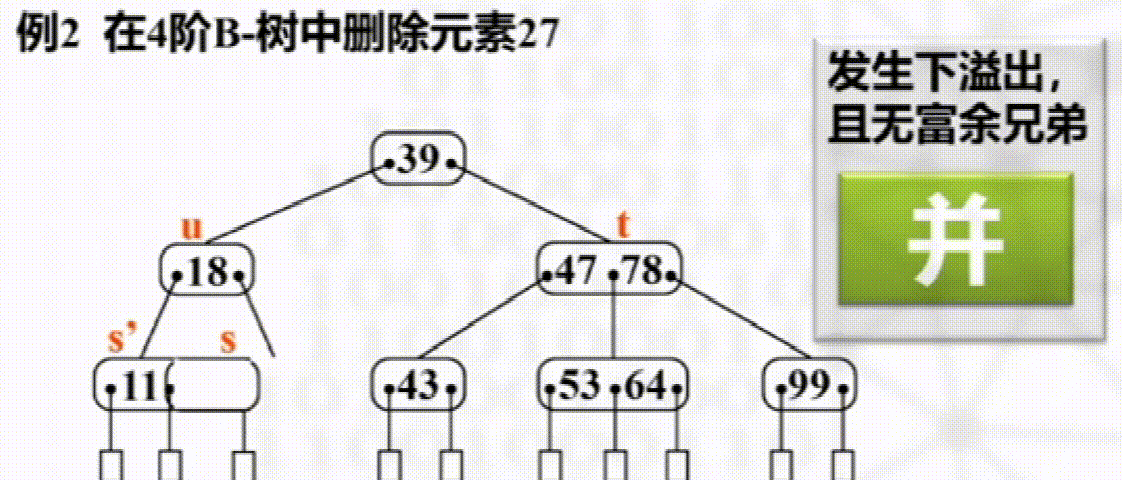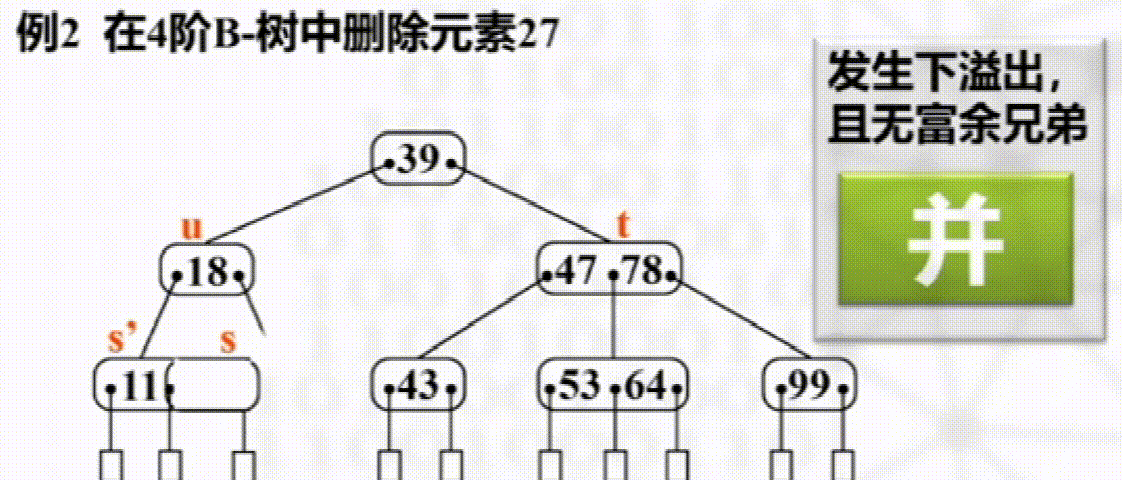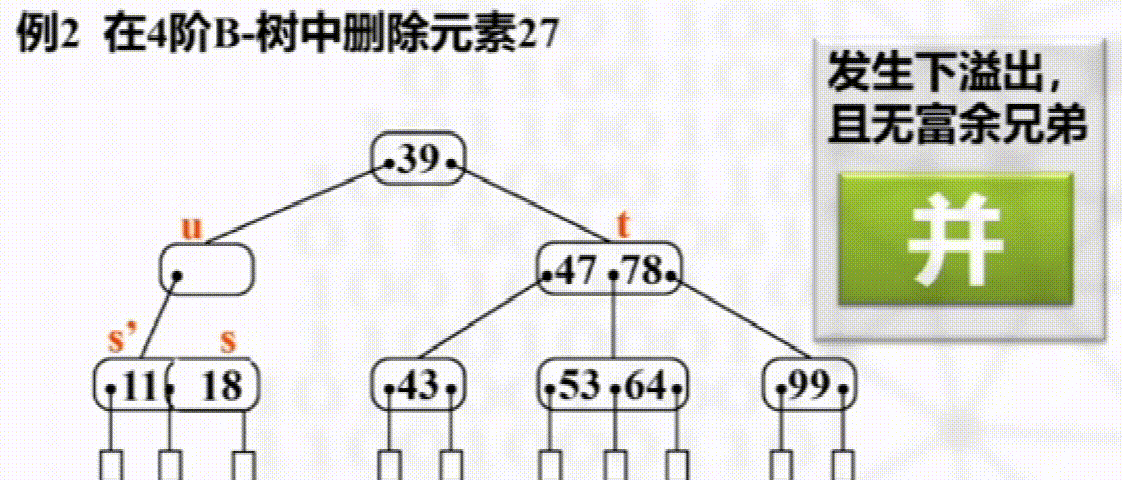
3. 如发生下溢出，则若其左右兄弟有多于$\dfrac{m}{2}$个元素，则向其接一个元素

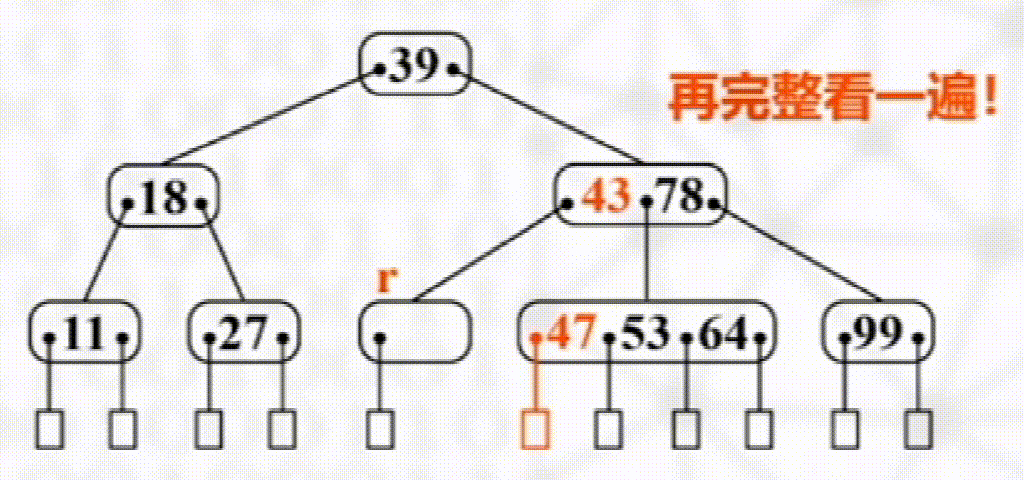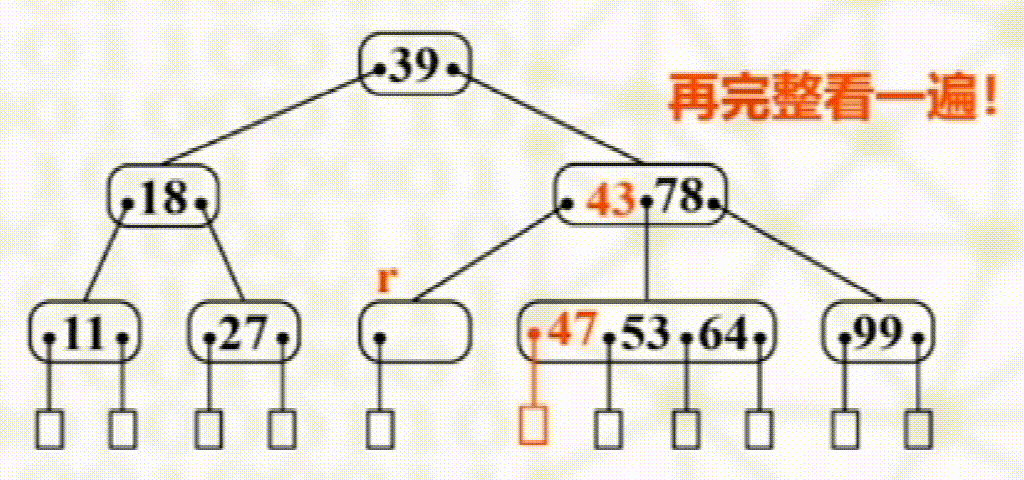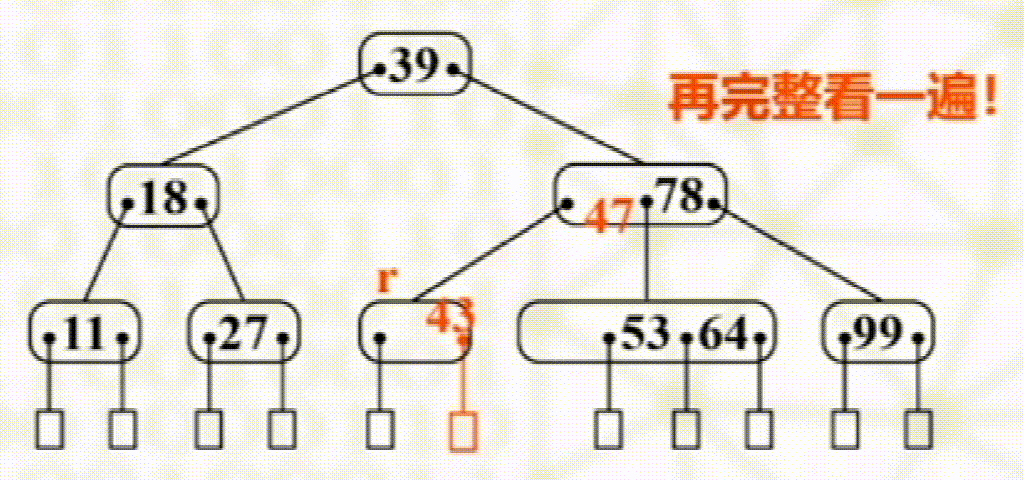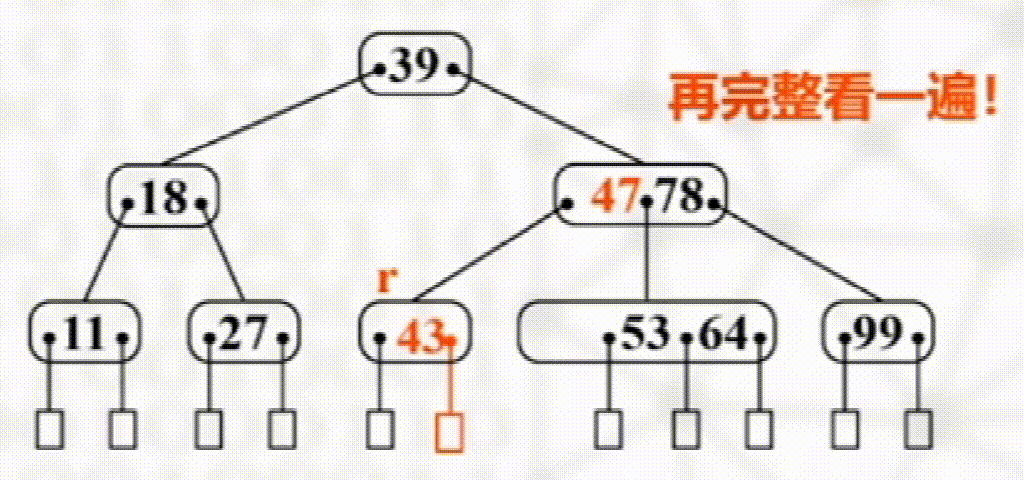
4. 没有富余兄弟，与兄弟合并且将两结点之间元素下移

   

B+树

• 每个分支结点最多有$m$棵子树
• 非叶根结点至少有2棵子树，其他每个分支结点至少有$[\dfrac{m}{2}]$棵子树
• 结点的子树与关键字个数相等
• 所有叶子结点包括全部关键字及指向相应记录的指针，叶结点按大小顺序排列，且相邻叶结点按大小顺序相互连接
• 所有分支结点中仅包含各个子结点中关键字最大值及其子结点的指针
  应用

应用：文件索引、数据库索引

B+树 & B树

B+树	B树
具有$n$个关键字结点只含有$n$棵子树 每个关键字对应一棵子树	具有$n$个关键字结点含有$n+1$棵子树
每个结点关键字个数：$[\dfrac{m}{2}]\le n\le m$ (根结点：$1\le n\le m$)	每个结点关键字个数：$[\dfrac{m}{2}]-1\le n\le m-1$ (根结点：$1\le n\le m-1$)
非叶结点只包含索引信息	非叶结点包含关键字信息
叶结点包含所有关键字，包括非叶节点的关键字	叶结点关键字和非叶结点关键词不重复
支持顺序查找	不支持顺序查找

散列表

散列函数（$h,hash$）:存储关键字($key$)和存储位置($Loc$)之间关系

• 冲突：$key_1{\neq}key_2$,$h(key_1)=h(key_2)$
• 同义词：对给定$h$，具有相同散列值不同数字
• 堆积：同义词和非同义词冲突

常见散列函数

除留余数法

$h(key)=key%M$

==模值取不超过$M$的素数$P$更好==

不足

1. 存在不动点$h(0)=0$,与均分布相悖
2. 相邻的关键字散列到相邻地址

除留余数法改进MAD

$h(key)=(key*a+b)%P$

• $b$作为偏移量，消除了不动点
• $a$作为间隔量，原本相邻地址变成间隔$a$

平方取中法

$h(key)=(key)^2$的中间若干位

• 位数$k$满足：$10^{k-1}{\leq}n{\leq}10^k$

  $n$为集合中元素个数

折叠法

1. 折叠法自左到右，分为位数相等几部分，每部分位数与散列表地址相同
2. 将数据叠加

冲突处理技术

聚集主要原因：解决冲突方法选择不断

• 开散列法

  存储主表之外

• 闭散列法

  存储主表之内

拉链法

存储方式

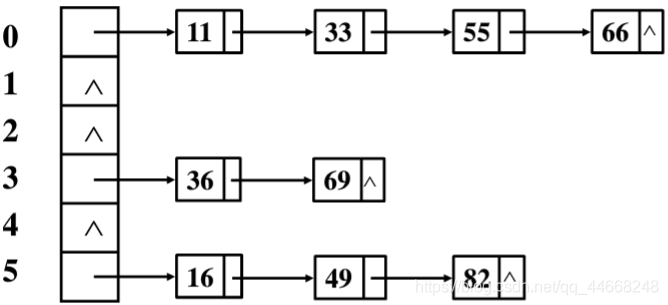
时间复杂度

• 查找：$O(\dfrac{n}{M})$
• 插入：$O(\dfrac{n}{M})$
• 删除：$O(\dfrac{n}{M})$

线性探查法

开放地址法

解决方式：$h_i=(h(key)+i)modM$

聚集问题：线性聚集

二次探查法

开放地址法

解决方式：$h_{2i-1}=\left(h\left(key\right)+i^2\right)\text{mod}M\\h_{2i}=\left(h\left(key\right)-i^2\right)\text{mod}M$

聚集问题：二次聚集

双散列法

开放地址法

解决方式：$H_{i}=(h_1(key)+ih_2(key))modM$

聚集问题：二次聚集

性能分析

状态因子$\alpha$：$\alpha=\dfrac{表中记录数n}{散列表长度m}$

冲突处理方法	解决方式	开/闭散列法	冲突问题	成功搜索长度	失败搜索长度
拉链法	/	开散列法	无	$1+\dfrac{\alpha}{2}$	$\alpha+e^{-\alpha}$
线性探查法	$h_i=(h(key)+i)modM$	开放地址法	线性聚集	$\dfrac{1}{2}(1+\dfrac{1}{1-\alpha})$	$\dfrac{1}{2}(1+\dfrac{1}{(1-\alpha)^2})$
二次探查法	$h_{2i-1}=(h(key)+i^2)modM$ $h_{2i}=(h(key)-i^2)modM$	开放地址法	二次聚集	$-\dfrac{1}{\alpha}\log_e(1-\alpha)$	$-\dfrac{1}{1-\alpha}$
双散列法	$H_{i}=(h_1(key)+ih_2(key))modM$	开放地址法	/	$-\dfrac{1}{\alpha}\log_e(1-\alpha)$	$-\dfrac{1}{1-\alpha}$

减少冲突方法：

1. 减少装填因子$\alpha$
2. 设计冲突少的散列函数
3. 处理冲突时避免产生聚集现象

总结与考点

搜索长度

	搜索成功	搜索失败
无序表顺序搜索	$\dfrac{n+1}{2}$	$n+1$
有序表顺序搜索	$\dfrac{n+1}{2}$	$\dfrac{n}{2}+{\dfrac{n}{n+1}}$
对半搜索	$S_{success}=1+n+\dfrac{n+2(1-2^n)}{N}$ $N=2^n-1+k$	$S_{fail}=n+\dfrac{2k}{N+1}$